meet in the middle——折半搜索算法
meet in the middle——折半查找算法
提出问题
回溯法是一个很经典的算法了,也可以视为暴力搜索算法,一般时间复杂度会达到指数级甚至阶乘级,只能用于求解规模很小的问题。比如N皇后问题、迷宫问题、数独、0-1背包……当问题规模变大一些时,一般会考虑是否有重复搜索,尝试通过记忆化来剪枝,使其变为记忆化搜索,来减少子问题的重复搜索次数,比如爬台阶,这样的做法使时间复杂度达到与动态规划相同的量级,不过常数更大。
考虑这样一个问题:给定一个长度为n的数组,里面有正有负。现在想从表中选出任意多个数,使它们的和为0,问有多少种选法?
考虑退化问题,如果把要选出来的个数确定下来,比如为2、3、4……就变成经典问题——K数之和,暴力方法复杂度为O(N^k),通过排序+双指针可以达到O(N^(k-1))。然而一旦不确定,就变成了0-1背包,对每个数都要考虑选与不选,时间复杂度为O(2^N),才能找到所有组合。这一般能处理到N=20的情况,再大就无能为力了。
假如N=30,这种方法就完全不可行了吗?能否对上面的算法做一些优化呢?这就要用到本文说的meet in the middle算法了。
meet in the middle 简介
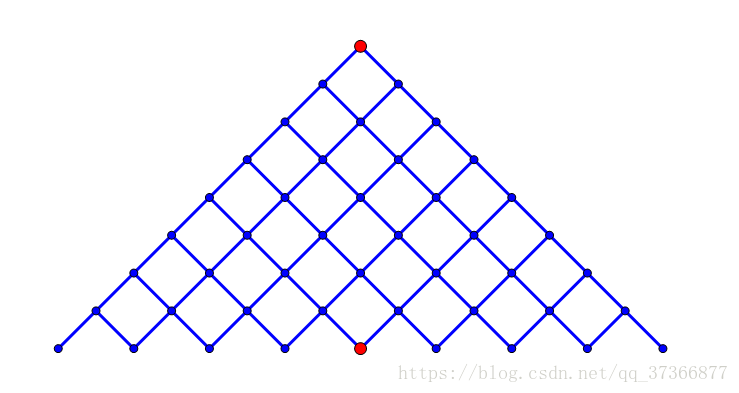
这部分内容参照了Meet in the Middle 算法。我们可以将dfs过程视为对状态树的搜索,如图所示。
假设从上面的红点开始进行搜索,找一条能通向下面那个红点的路径,每个点都有两条岔路可供选择。显然如果我们简单的从上面那个点开始BFS,代价是较大的,在最差的情况下,可能需要把整张图的45个节点给走一遍。当然把搜索的重任全部交给一个节点是不合理的。于是Meet in the Middle算法就诞生了。顾名思义,就是两个节点各自向中间搜索,直至碰头。
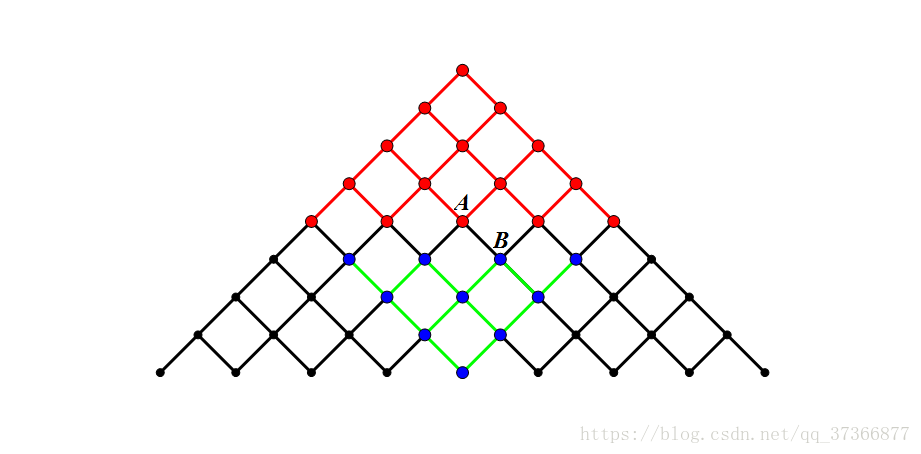
在上图中红点的部分为起点开始向外搜索到的点,而蓝点表示从终点开始搜索到的点,假如此时搜索进行到点B,直接就能发现A点是从起点过来的点,那么也就自然找到了一条从 起点->A->B->终点 的路径。考虑最坏的情况,红点的搜索范围我们人为规定为层数的一半,而蓝点的搜索范围实际上是从它本身开始向上分叉,类似于红点搜索范围的轴对称图形,这样,整个图里面黑色部分的节点与边其实我们都可以不用访问,这就起到了剪枝的作用。
例题
开始的问题
考虑最开始的问题,我们可以将数组一分为二,先搜索前一半,并用哈希表记录所有能得到的值,这相当于先让上图中的点A对搜索范围进行整个搜索,这部分的时间复杂度是O(2^(n/2))的。接着,我们对后一半进行搜索,并对得到的每一个结果,尝试在上面的哈希表中找到它的相反数,如果找到,就说明搜索成功。这类似于B从底往上搜索,并检查是否与A相遇,也就是meet in the middle的过程。搜索B的时间复杂度是O(2^(n/2))的,而查哈希表的时间是O(1)的,所以这部分也是O(2^(n/2))的,总的时间复杂度就是O(2*2^(n/2)),不过,最好时间复杂度也是O(2^(n/2)),因为我们总是会搜索A的全部范围。
下面来看力扣上的两个应用。
494. 目标和 - 力扣(LeetCode)
题目描述
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
解答
其实,这道题可以直接用dfs来解决,并不会超时(毕竟数据范围只有20),用时1200ms,代码如下
1 | //dfs,2^20大概为1e6 |
不过,我们也可以用meet in the middle来进行优化,实际上码量差不多,然而用时仅为16ms,代码如下
1 | //用meet in the middle进行优化,复杂度O(2*2^(n/2)),约为5000,但常数较大 |
805. 数组的均值分割 - 力扣(LeetCode)
题目描述
给定你一个整数数组 nums
我们要将 nums 数组中的每个元素移动到 A 数组 或者 B 数组中,使得 A 数组和 B 数组不为空,并且 average(A) == average(B) 。
如果可以完成则返回true , 否则返回 false 。
注意:对于数组 arr , average(arr) 是 arr 的所有元素的和除以 arr 长度。
示例 1:
输入: nums = [1,2,3,4,5,6,7,8] 输出: true 解释: 我们可以将数组分割为 [1,4,5,8] 和 [2,3,6,7], 他们的平均值都是4.5。
示例 2:
输入: nums = [3,1] 输出: false
提示:
1 <= nums.length <= 300 <= nums[i] <= 104
解答
这道题的数据范围,就非用meet in the middle不可了,不过还不是一道裸题,还得加以推理,实际上不愧为一道hard。
两个数组平均值相同,那么它们相加后的平均值不变,所以分成的两个数组平均值都与原数组相等
将所有数-原来的平均值,需要找到一个数组,它的和为0
为了避免浮点数,将所有数乘以nums.size()
然而,这样的做法复杂度为O(2^N),超时了,59/111
改进:我们将数组一分为二,分别计算两个部分能形成的和,看看有没有相反数,优化到O(2^(N/2)),用时52ms
1 | class Solution { |