离散优化算法解题报告
思路
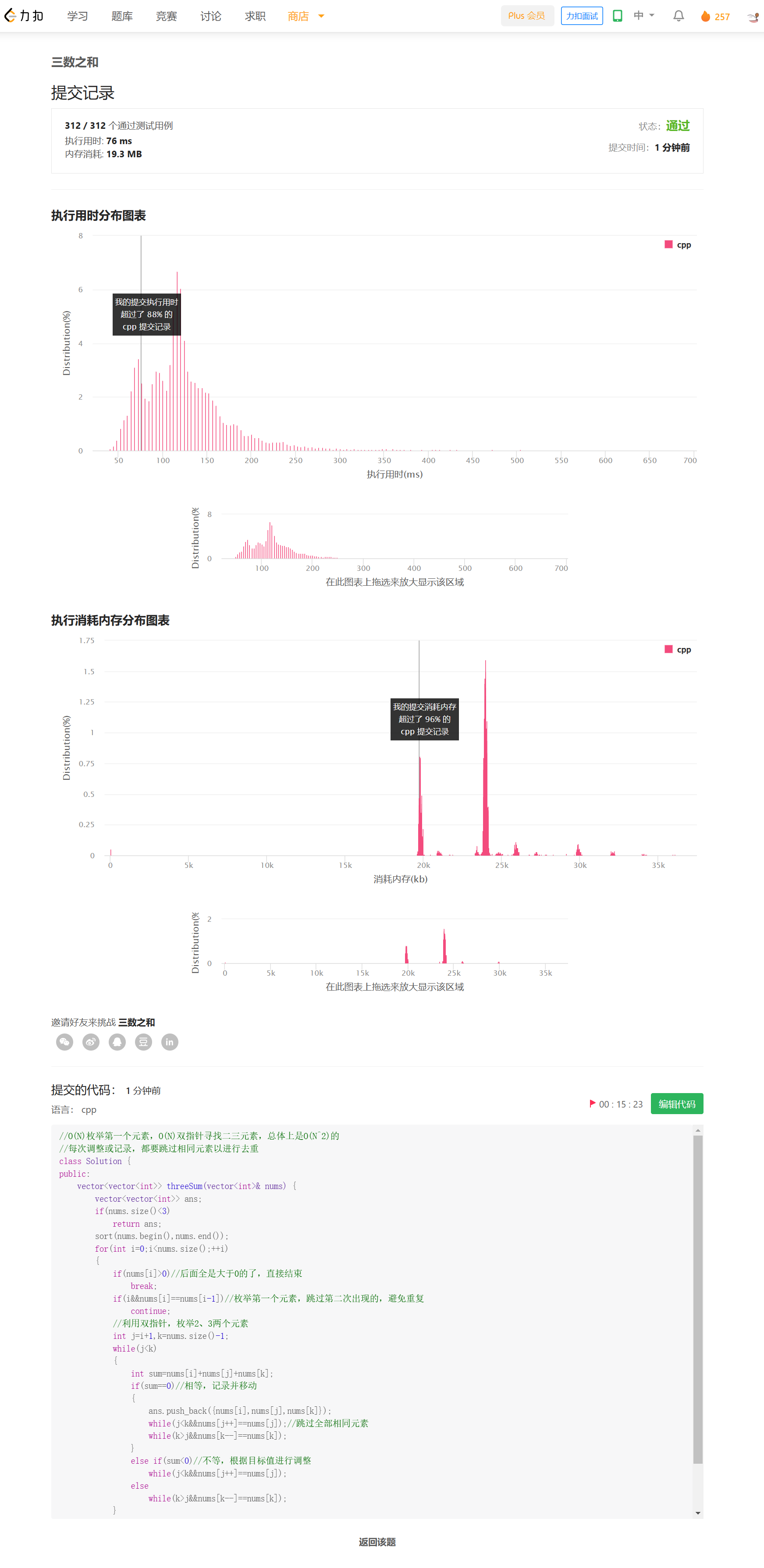
for循环枚举第一个元素nums[i],并利用双指针在后面的元素中寻找nums[j]+nums[k]==-nums[i],在和更小时,增大nums[j],否则减小nums[k],要通过排序使nums有序,便于双指针移动。
排序的复杂度为O(NlogN),枚举+双指针复杂度为O(N^2)。
去重问题:枚举i时,相同的只枚举第一个;双指针过程中,每次记录和调整都直接跳过相同元素。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> ans;
sort(nums.begin(),nums.end());
for(int i=0;i<nums.size();++i)
{
if(nums[i]>0)
break;
if(i&&nums[i]==nums[i-1])
continue;
int j=i+1,k=nums.size()-1;
while(j<k)
{
int sum=nums[i]+nums[j]+nums[k];
if(sum==0)
{
ans.push_back({nums[i],nums[j],nums[k]});
while(j<k&&nums[j++]==nums[j]);
while(k>j&&nums[k--]==nums[k]);
}
else if(sum<0)
while(j<k&&nums[j++]==nums[j]);
else
while(k>j&&nums[k--]==nums[k]);
}
}
return ans;
}
};
|
提交记录
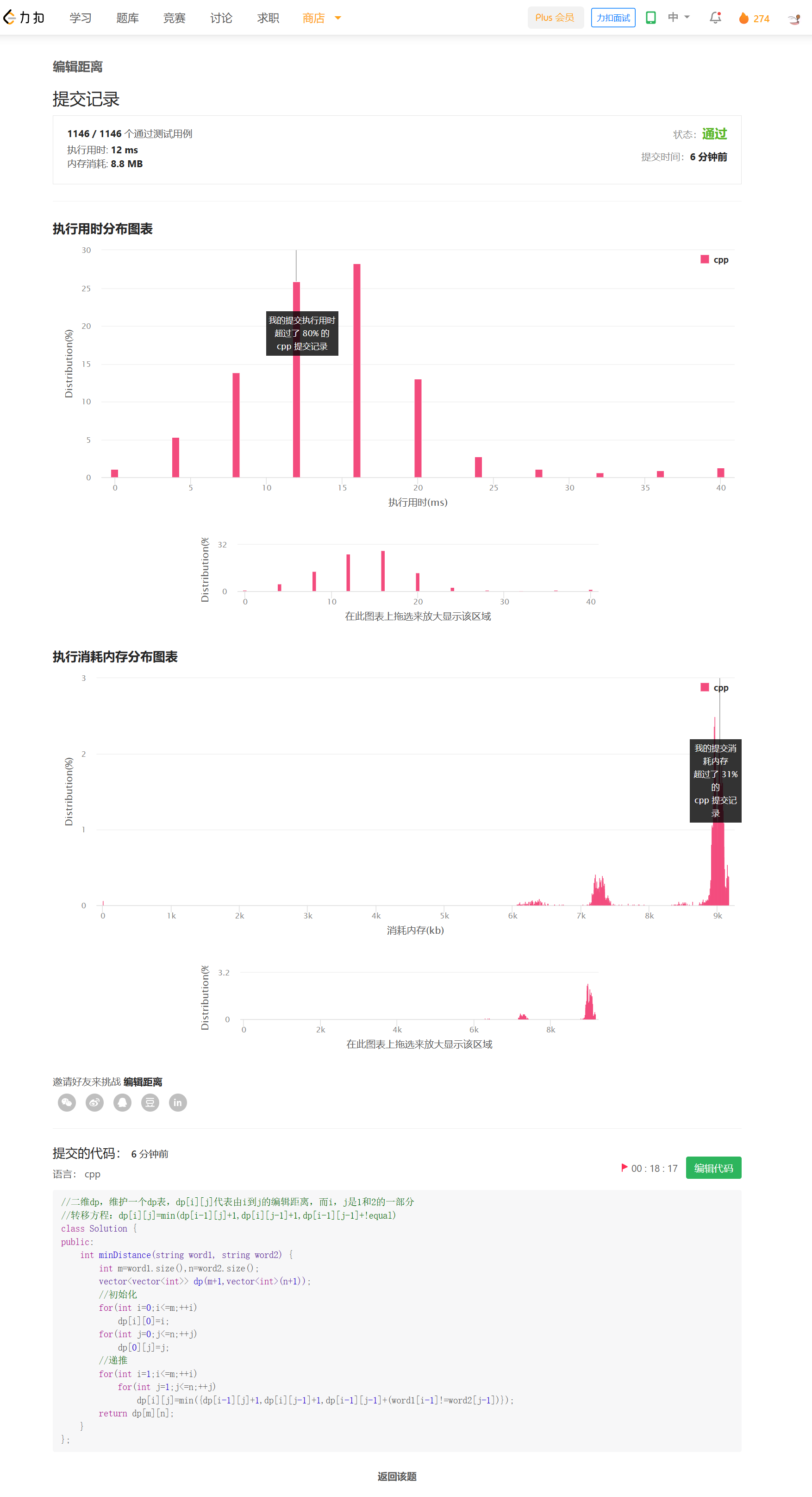
思路——动态规划
根据课上讲的思路,维护一张二维dp表。
dp[i][j]代表i和j状态之间的编辑距离(具体来说,是s[0..i-1]与t[0..j-1]之间的编辑距离)
状态转移方程:dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+!equal)
dp[n][m]就是答案。时间复杂度O(MN),空间复杂度O(MN)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
int minDistance(string word1, string word2) {
int m=word1.size(),n=word2.size();
vector<vector<int>> dp(m+1,vector<int>(n+1));
for(int i=0;i<=m;++i)
dp[i][0]=i;
for(int j=0;j<=n;++j)
dp[0][j]=j;
for(int i=1;i<=m;++i)
for(int j=1;j<=n;++j)
dp[i][j]=min({dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+(word1[i-1]!=word2[j-1])});
return dp[m][n];
}
};
|
提交记录
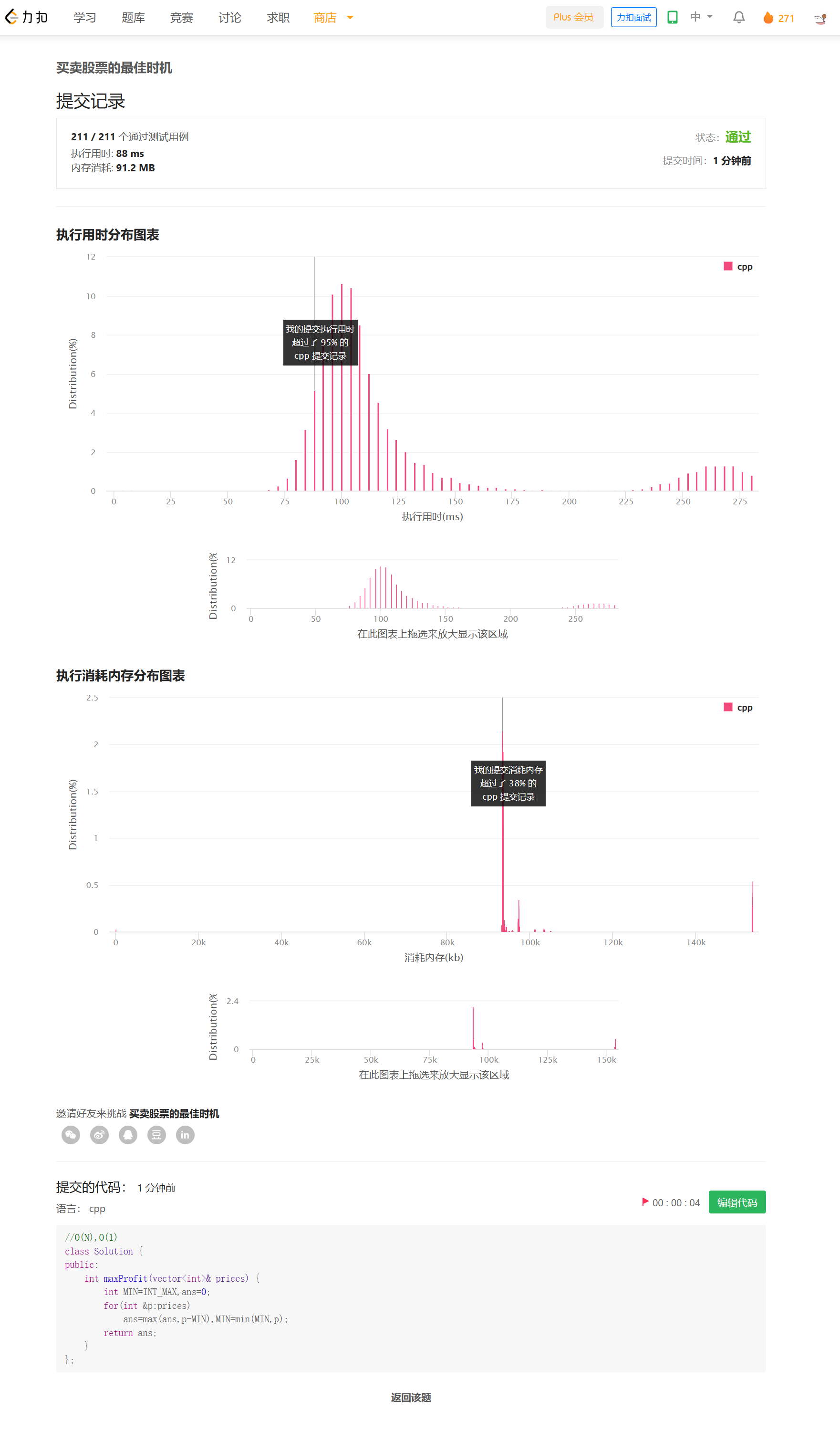
思路
一次遍历,假设我们在i处卖出,那最佳的买入时间就是0~i中最便宜的时候。
所以我们维护一个MIN,记录前面的最小值即可。
代码
1
2
3
4
5
6
7
8
9
10
|
class Solution {
public:
int maxProfit(vector<int>& prices) {
int MIN=INT_MAX,ans=0;
for(int &p:prices)
ans=max(ans,p-MIN),MIN=min(MIN,p);
return ans;
}
};
|
提交记录
思路
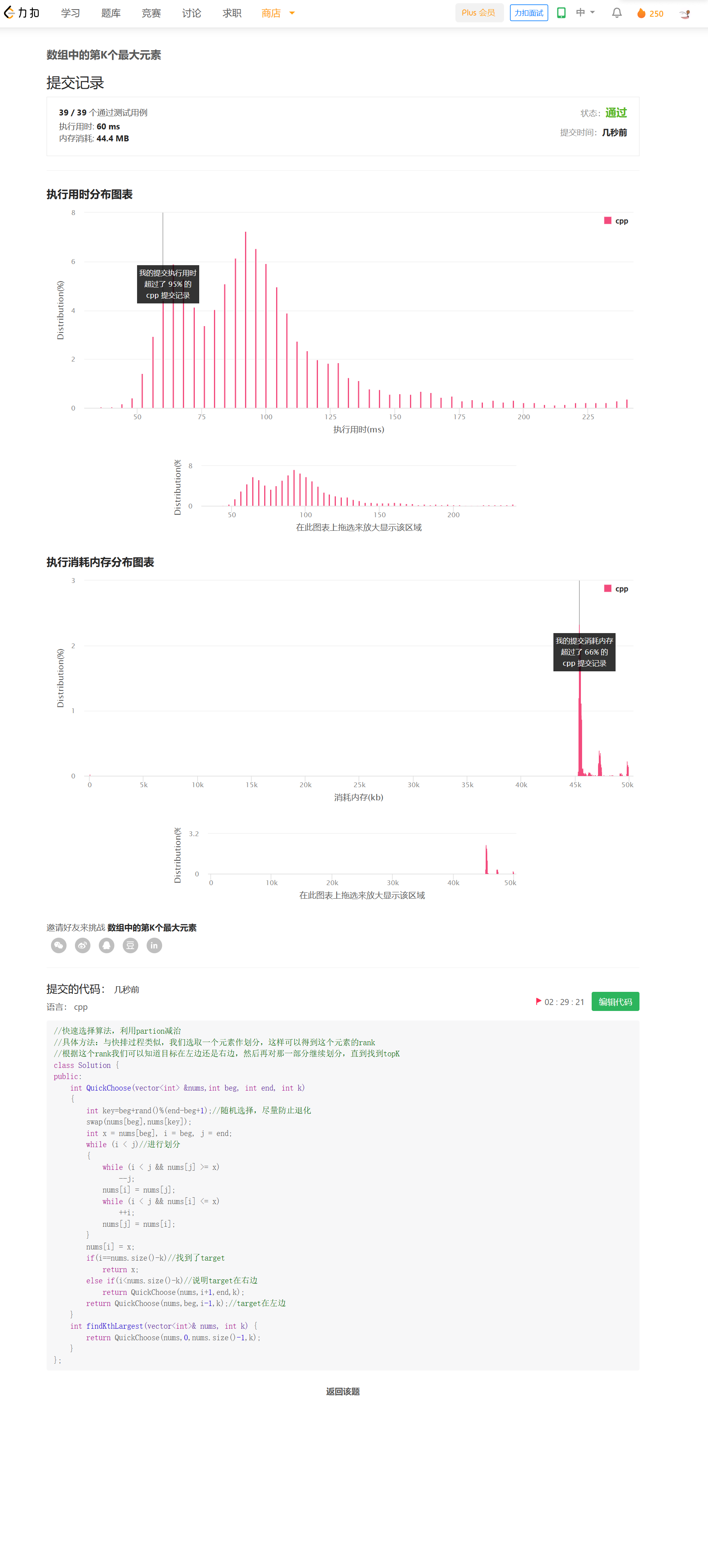
在快速排序的一个划分中,我们可以知道枢轴在数组中的rank,假如从小到大排,后面有k-1个元素,那它就是第k大的元素。我们根据已经得到的元素,可以确定target的位置在哪一半,然后再对那一半递归地执行这个过程,直到找到target。
快速选择算法,与快速排序的划分方式相同,区别的是只对目标所在区域继续划分,这样下来,平均时间复杂度是O(N)的,不过最坏时间复杂度是O(N^2)的,为了避免退化,采用随机选取枢轴的方法。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
int QuickChoose(vector<int> &nums,int beg, int end, int k)
{
int key=beg+rand()%(end-beg+1);
swap(nums[beg],nums[key]);
int x = nums[beg], i = beg, j = end;
while (i < j)
{
while (i < j && nums[j] >= x)
--j;
nums[i] = nums[j];
while (i < j && nums[i] <= x)
++i;
nums[j] = nums[i];
}
nums[i] = x;
if(i==nums.size()-k)
return x;
else if(i<nums.size()-k)
return QuickChoose(nums,i+1,end,k);
return QuickChoose(nums,beg,i-1,k);
}
int findKthLargest(vector<int>& nums, int k) {
return QuickChoose(nums,0,nums.size()-1,k);
}
};
|
提交记录
思路
理解题意:我们所要返回的结果,实际上是高度变化时的横纵坐标。
所以可以从左到右遍历各个顶点,并实时维护高度,当最大高度变化时,返回当前的横坐标和新高度。
为了从左到右遍历,我们要先对横纵坐标进行排序,此时要注意横坐标重合的情况,为了保证先添加最大坐标,先删除最小坐标(防止添加或删除时的高度连续变化也被添加到答案),左端点相同,应该高的在前,右端点相同,应该矮的在前,所以在构造端点对时,如果是左端点,将高度取负存入,这样既能区分又方便排序。
为了维护高度并实时获得最大高度,可以选用multiset,在logN的时间内进行删除、插入和查找。
总的时间复杂度为O(NlogN)。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public:
vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
vector<pair<int,int>> points;
vector<vector<int>> ans;
for(auto&v:buildings)
points.push_back({v[0],-v[2]}),points.push_back({v[1],v[2]});
sort(points.begin(),points.end());
multiset<int> height;
int pre=0;
for(auto&[x,y]:points)
{
if(y<0)
height.insert(-y);
else
height.erase(height.find(y));
int now=height.empty()?0:*height.rbegin();
if(now!=pre)
ans.push_back({x,now}),pre=now;
}
return ans;
}
};
|
提交记录

方法一——哈希表
思路
用哈希表cnt记录nums1中数字出现的个数,然后遍历nums2,如果计数大于0,则存入ans,并且--cnt。
为减小哈希表的空间消耗,如果nums1更大,则交换nums1和nums2。
时间复杂度O(M+N),空间复杂度O(min(M,N))。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
unordered_map<int,int> cnt;
if(nums1.size()>=nums2.size())
swap(nums1,nums2);
for(int &num:nums1)
++cnt[num];
vector<int> ans;
for(int &num:nums2)
if(cnt[num])
ans.push_back(num),--cnt[num];
return ans;
}
};
|
提交记录
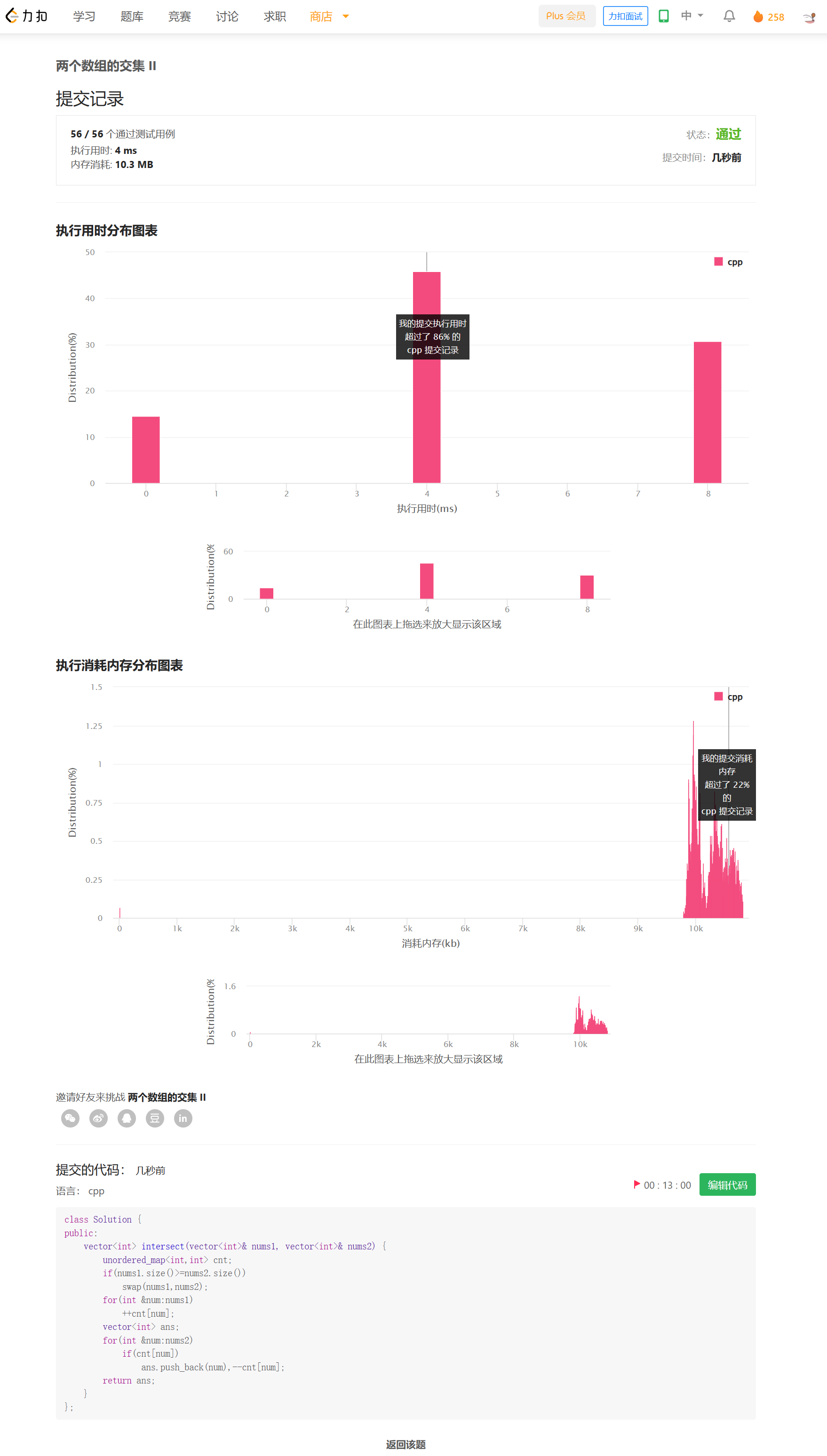
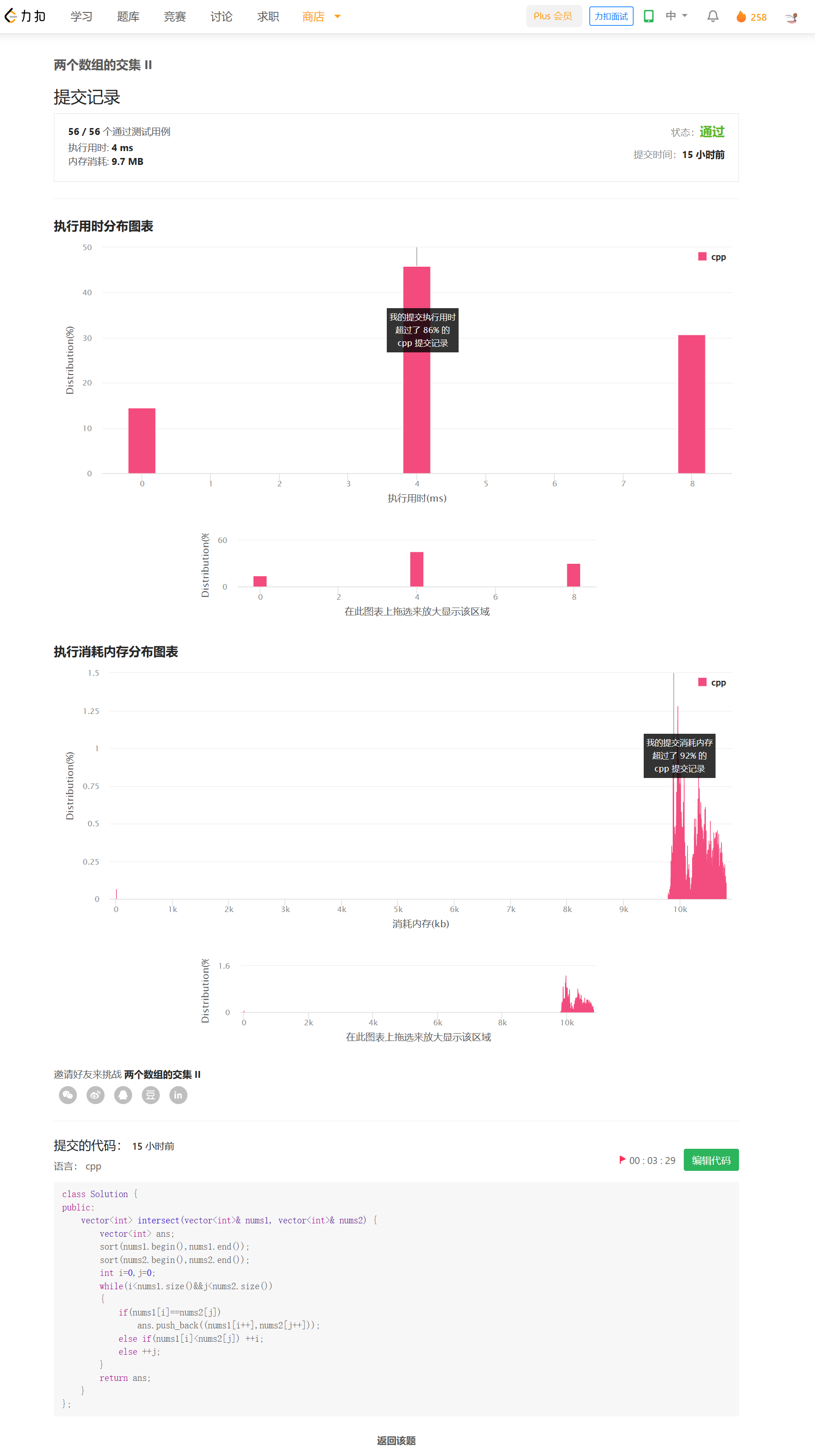
方法二——排序+双指针
思路
排序后,可以使用类似于合并两个有序数组的方法。通过双指针在O(M+N)时间内完成。
时间复杂度来自于排序。时间复杂度O(mlogm+nlogn),空间复杂度O(min(M,N))。复杂度比上面高,但实际运行销量反而更快。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
vector<int> ans;
sort(nums1.begin(),nums1.end());
sort(nums2.begin(),nums2.end());
int i=0,j=0;
while(i<nums1.size()&&j<nums2.size())
{
if(nums1[i]==nums2[j])
ans.push_back((nums1[i++],nums2[j++]));
else if(nums1[i]<nums2[j]) ++i;
else ++j;
}
return ans;
}
};
|
提交记录
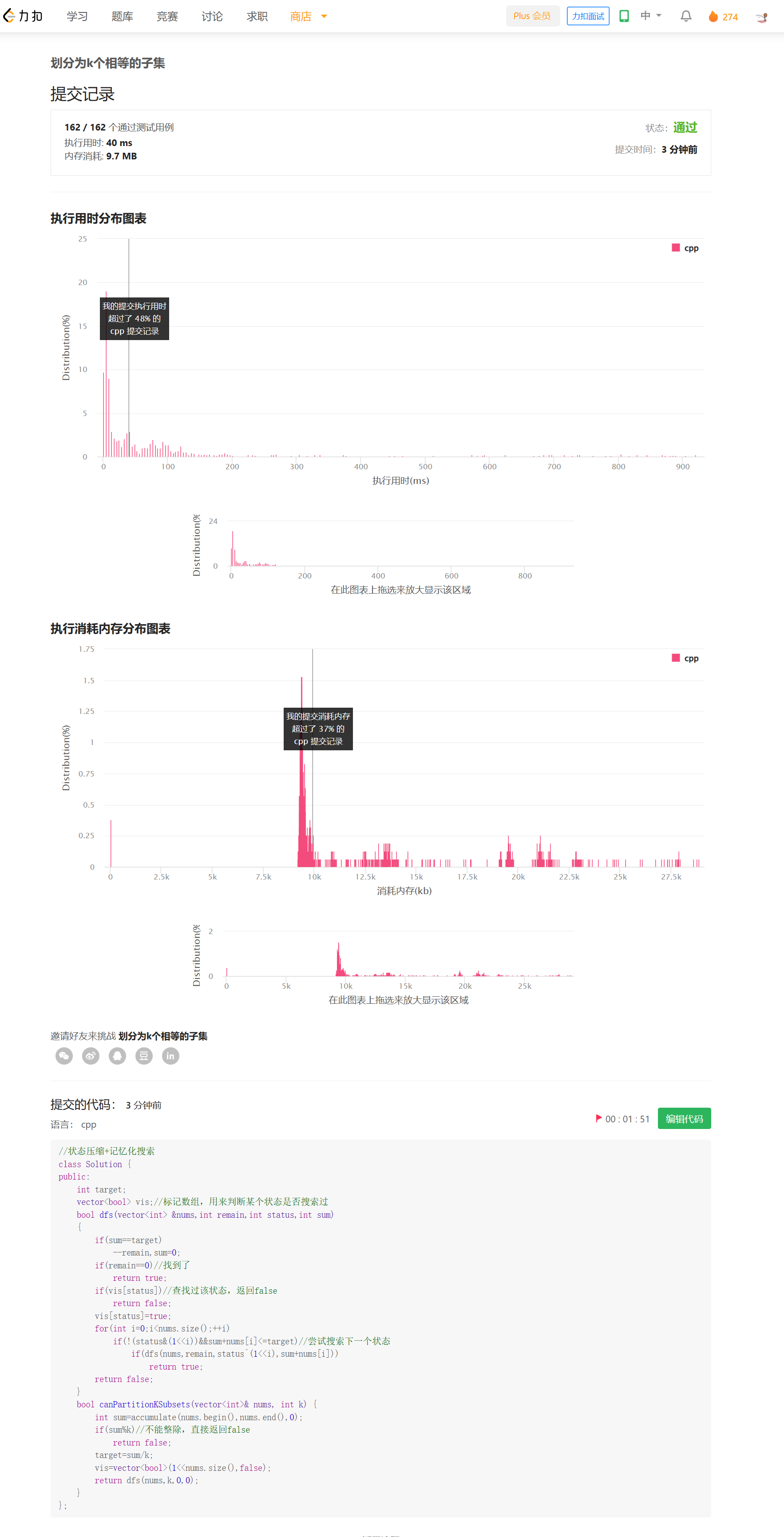
思路——搜索+可行性剪枝
首先,可以很容易地写出搜索算法,具体来说,是维护一个状态变量status,一个剩余要找的子集remain,一个当前子集元素和sum。目标是找到sum==target的子集,然后--remain,如果remain=0,就说明可以,如果找遍了也没有,就返回false。
但是暴力搜索会超时,我们要进行剪枝。
剪枝一——记忆化搜索
一种很普遍的思路是,将搜索过的状态记录下来,如果再碰到这种状态,就直接返回,具体来说,我们维护一个vis数组,大小为2^n,记录所有可能的状态是否搜索过,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public:
int target;
vector<bool> vis;
bool dfs(vector<int> &nums,int remain,int status,int sum)
{
if(sum==target)
--remain,sum=0;
if(remain==0)
return true;
if(vis[status])
return false;
vis[status]=true;
for(int i=0;i<nums.size();++i)
if(!(status&(1<<i))&&sum+nums[i]<=target)
if(dfs(nums,remain,status^(1<<i),sum+nums[i]))
return true;
return false;
}
bool canPartitionKSubsets(vector<int>& nums, int k) {
int sum=accumulate(nums.begin(),nums.end(),0);
if(sum%k)
return false;
target=sum/k;
vis=vector<bool>(1<<nums.size(),false);
return dfs(nums,k,0,0);
}
};
|
提交记录:
剪枝二——多个可行性剪枝
实际运行效果并不是特别好,经过分析,保留所有2^n个状态并不是必要的,可以有选择地间断保留,同时可以通过规定选择顺序进行剪枝,以及其余一些可行性剪枝,总结如下:
- 在进行一个子集搜索时,指针只进不退,这样可以排除子集内部的全排列。实现方法是传递一个
start,只从start开始选择,当搜索下一个子集时,再将start归零。
- 保留子集形成时的状态,这样可以排除子集之间的全排列。实现方法是在子集形成时用哈希表对状态进行记录,在下一次形成时进行比对,如果保存过,就不继续搜索,这实际上是间断地保存状态,可以大大减小保留的状态数。
- 可行性剪枝一:先对数组进行排序,正序搜索,如果
sum+nums[i]>target,就可以中止了,因为后面的一定更大。
- 可行性剪枝二:数组排序后,相同元素聚集,在搜索一个元素失败后,后面与它相同的元素也一定失败,可以直接跳过。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
public:
int target;
unordered_set<int> vis;
bool dfs(vector<int> &nums,int remain,int status,int sum,int start)
{
if(sum==target)
{
if(vis.find(status)!=vis.end())
return false;
vis.insert(status);
return dfs(nums,remain-1,status,0,0);
}
if(remain==0)
return true;
for(int i=start;i<nums.size();++i)
{
if(nums[i]+sum>target)
break;
if(!(status&(1<<i))&&sum+nums[i]<=target)
{
if(dfs(nums,remain,status^(1<<i),sum+nums[i],i+1))
return true;
while(i<nums.size()-1&&nums[i+1]==nums[i]) ++i;
}
}
return false;
}
bool canPartitionKSubsets(vector<int>& nums, int k) {
int sum=accumulate(nums.begin(),nums.end(),0);
if(sum%k)
return false;
target=sum/k;
sort(nums.begin(),nums.end());
return dfs(nums,k,0,0,0);
}
};
|
提交记录:
思路——动态规划
设dp[i][0]表示手中没有股票的最大收益,dp[i][1]表示手中有股票的最大收益。
状态转移方程:
dp[i][0] & = max(dp[i-1][0],dp[i-1][1]+prices[i]-fee)
dp[i][1] & = max(dp[i-1][1],dp[i-1][0]-prices[i])
由于当前状态仅与前一个状态有关,可以省略数组,直接使用两个pair进行转移
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n=prices.size();
pair<int,int> pre={0,-prices[0]},next;
for(int i=1;i<n;++i)
{
next.first=max(pre.first,pre.second+prices[i]-fee);
next.second=max(pre.second,pre.first-prices[i]);
pre=next;
}
return pre.first;
}
};
|
提交记录
方法一——Floyd+记忆化搜索/动态规划
思路
既然是要找到访问所有节点的最短路径,我们可以对这个过程进行分解,变为如下两步。
- 首先,找到所有点对之间的最短路,这是一个多源点最短路问题,可以用Floyd算法在
O(N^3)时间内解决
- 然后,对这些点对做一个全排列,计算每一种排列的路径和,找到最小值。这是
O(N!)的时间复杂度。
在N=12时,N!是会超时的,考虑如何优化。
Floyd的预处理是不可省略的,实际上O(N^3)在N=12时也不是算法性能的制约。但是第二个过程可以用动态规划或者记忆化搜索进行优化。写成递归形式的记忆化搜索比较直观,memo[v][status]代表所在点为v,状态为status时所用的最短路径。(status的每一位代表某个点是否被访问,这是状态压缩的思想)。
最终时间复杂度为O(N^3+N^2*2^N)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public:
vector<vector<int>> memo,graph;
int ans=INT_MAX;
void dfs(int status,int now,int pre)
{
if(status==(1<<graph.size())-1)
ans=min(ans,now);
if(memo[status][pre]&&memo[status][pre]<=now)
return ;
memo[status][pre]=now;
for(int i=0;i<graph.size();++i)
if((status&(1<<i))==0)
dfs(status^(1<<i),now+graph[pre][i],i);
}
int shortestPathLength(vector<vector<int>>& graph1) {
int n=graph1.size();
graph=vector<vector<int>>(n,vector<int>(n));
for(int i=0;i<n;++i)
for(int &j:graph1[i])
graph[i][j]=1;
for(int i=0;i<n;++i)
for(int j=0;j<n;++j)
for(int k=j+1;j!=i&&k<n;++k)
if(graph[j][i]&&graph[i][k]&&(!graph[j][k]||graph[j][i]+graph[i][k]<graph[j][k]))
graph[j][k]=graph[k][j]=graph[j][i]+graph[i][k];
memo=vector<vector<int>>(1<<n,vector<int>(n));
for(int i=0;i<n;++i)
dfs(1<<i,0,i);
return ans;
}
};
|
提交记录
方法二——复合状态BFS
思路
广度优先搜索是寻找一条最短路径的常用方法,不过由于本题的特殊性,广度优先搜索的节点不是当前所在位置(v),而是位置和状态的组合(v,status),将这个组合存入队列中,展开搜索,最先找到的status=1<<n-1所经过的路径长度就是本题答案。
时间复杂度O(N^2*2^N)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public:
int shortestPathLength(vector<vector<int>>& graph) {
int n=graph.size(),length=0;
queue<pair<int,int>> q;
vector<vector<bool>> searched(n,vector<bool>(1<<n,false));
for(int i=0;i<n;++i)
q.push({i,1<<i}),searched[i][1<<i]=true;
while(true)
{
int cnt=q.size();
for(int i=0;i<cnt;++i)
{
auto [v,status]=q.front();
q.pop();
if(status==(1<<n)-1)
return length;
for(int &next:graph[v])
if(!searched[next][status|(1<<next)])
q.push({next,status|(1<<next)}),searched[next][status|(1<<next)]=true;
}
++length;
}
return -1;
}
};
|
提交记录
方法一:快速排序
思路
选取枢轴,将小的放到前面,大的放到后面。然后递归前一半和后一半。
不过很直接的快排会被卡掉,力扣给了两种极端样例——基本有序和基本相同。
为了处理基本有序的样例,枢轴应当是随机选取的,我们随机生成一个下标,然后与首元素进行交换,接着进行快排。
为了处理基本一致的样例,应当尽可能地让相同元素均匀分布在左右两侧,这样仍然是O(NlogN)的。比较简单的方法是频繁交换,也就是将交换条件由小于或大于改为小于等于或大于等于,这样最后枢轴就会落在中间。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public:
void QuickSort(vector<int> &nums,int beg, int end)
{
if (end <= beg)
return;
int key=beg+rand()%(end-beg+1);
swap(nums[beg],nums[key]);
int x = nums[beg], i = beg, j = end;
while (i < j)
{
while (i < j && nums[j] > x)
--j;
if(i<j)
nums[i++] = nums[j];
while (i < j && nums[i] < x)
++i;
if(i<j)
nums[j--] = nums[i];
}
nums[i] = x;
QuickSort(nums,beg, i - 1);
QuickSort(nums,i + 1, end);
}
vector<int> sortArray(vector<int>& nums) {
QuickSort(nums,0,nums.size()-1);
return nums;
}
};
|
提交结果
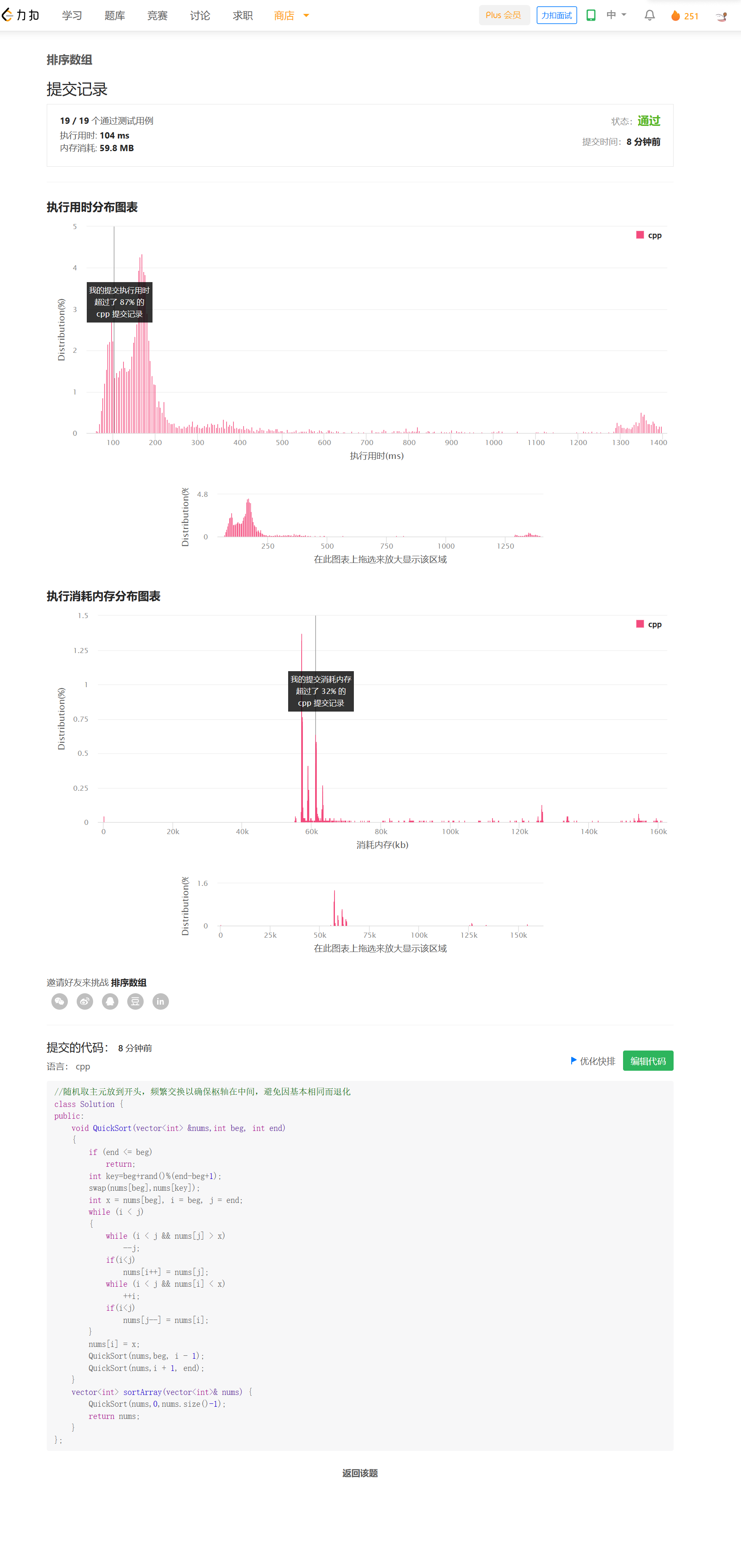
方法二——堆排序
思路
每次堆调整可以选出最大的元素,调换到最后使部分有序。一次堆调整为log(N),共计N次堆调整,这是O(NlogN)的,堆排序的最坏时间复杂度就是O(NlogN),所以不容易被卡掉。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public:
void heapAdjust(vector<int>& nums,int now, int end)
{
int x = nums[now];
for (int j = 2 * now + 1; j <= end; j = j * 2 + 1)
{
if (j < end && nums[j] < nums[j + 1])
++j;
if (x >= nums[j])
break;
nums[now] = nums[j], now = j;
}
nums[now] = x;
}
vector<int> sortArray(vector<int>& nums) {
int n = nums.size(), ans = 1, i = 0, end = nums.size() - 1;
for (int i = nums.size() / 2;i >= 0; --i)
heapAdjust(nums, i, nums.size() - 1);
swap(nums[0],nums[end]);
--end;
while (end > 0)
{
heapAdjust(nums,0, end);
swap(nums[0], nums[end]);
--end;
}
return nums;
}
};
|
提交结果
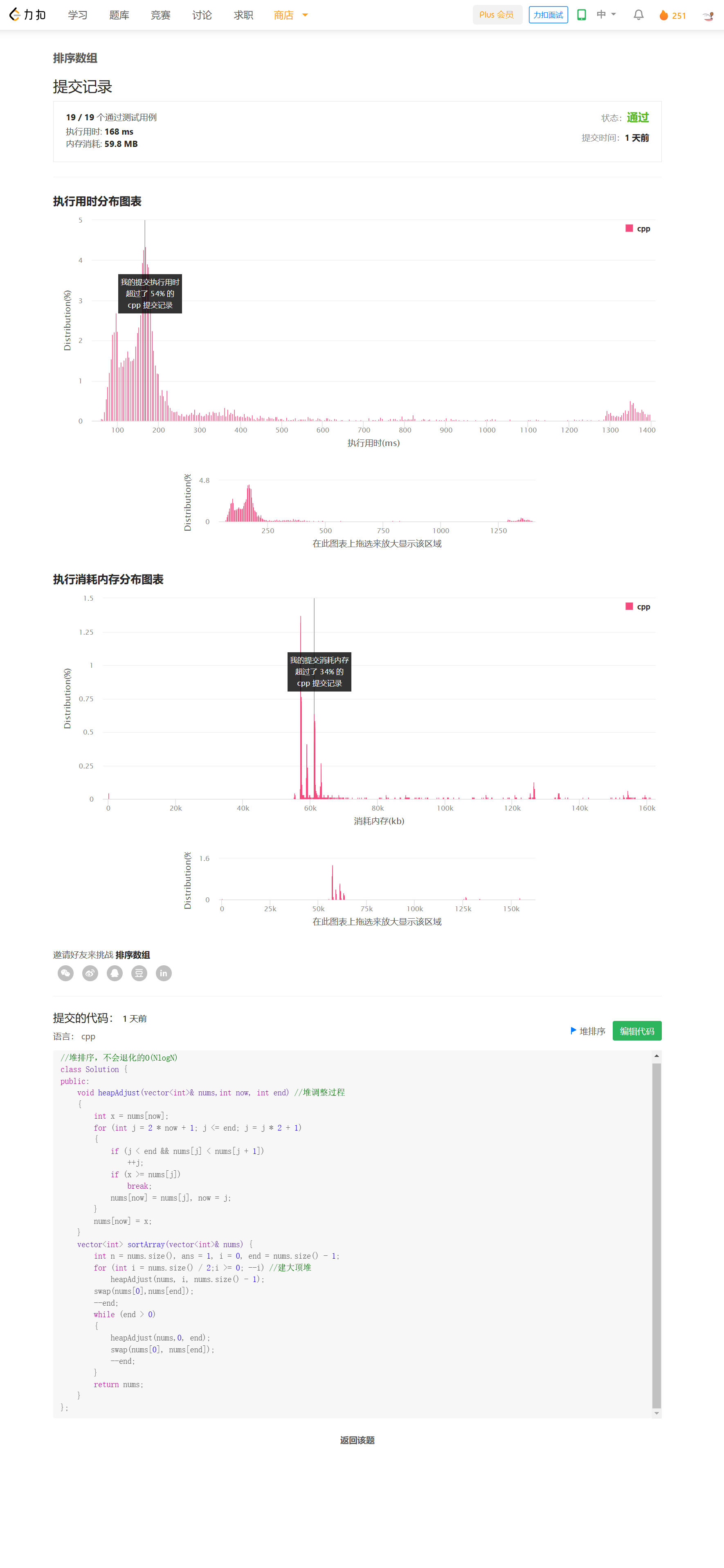
方法三——归并排序
思路
递归形式的二路归并,使用额外空间进行merge,最坏时间复杂度O(NlogN),也不容易被卡掉。不过需要额外申请tmp数组,产生O(N)的空间消耗,空间效率不高。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public:
void mergeSort(vector<int>&nums,vector<int>&tmp,int beg,int end)
{
if(beg>=end)
return ;
int mid=(beg+end)/2,i=beg,j=mid+1,pos=beg;
mergeSort(nums,tmp,beg,mid);
mergeSort(nums,tmp,mid+1,end);
while(i<=mid&&j<=end)
tmp[pos++]=nums[i]<nums[j]?nums[i++]:nums[j++];
while(i<=mid)
tmp[pos++]=nums[i++];
while(j<=end)
tmp[pos++]=nums[j++];
for(int i=beg;i<=end;++i)
nums[i]=tmp[i];
}
vector<int> sortArray(vector<int>& nums) {
vector<int> tmp(nums.size());
mergeSort(nums,tmp,0,nums.size()-1);
return nums;
}
};
|
提交结果
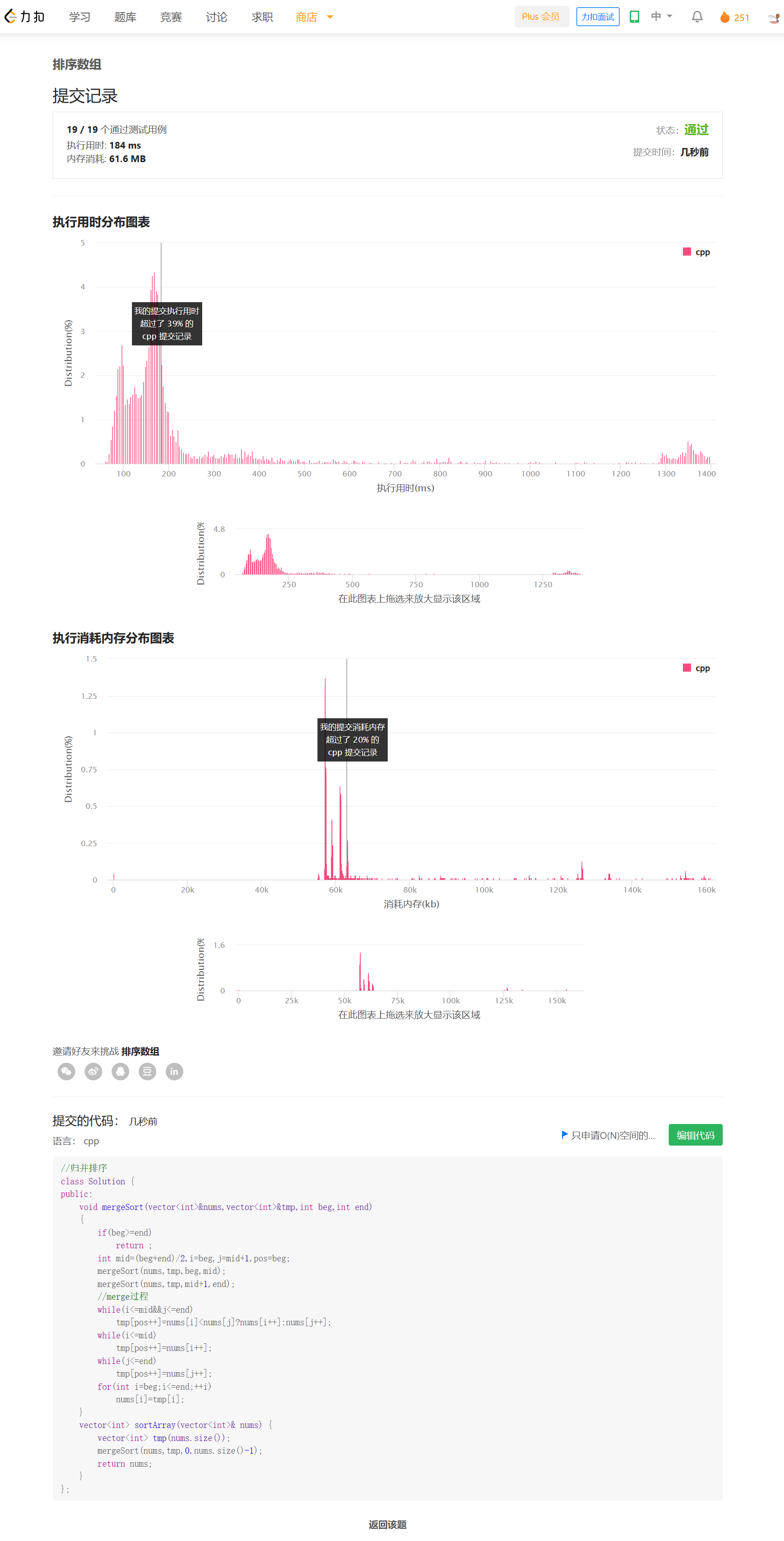
思路
贪心,每次使用不超过k的最大斐波那契数,就能得到最少的数目。
利用反证法简要证明:
代码
一种方法是预处理所有斐波那契数,然后二分找到不大于k的最大值,这种算法的时间复杂度是O(logklogN),空间复杂度为O(logN),实际上,可以直接通过递推的方法确定选择的斐波那契数,时间复杂度O(2*logk),空间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public:
int findMinFibonacciNumbers(int k) {
int a=1,b=1,ans=0;
while(b<=k)
{
a+=b;
swap(a,b);
}
while(k)
{
if(k>=b)
k-=b,++ans;
b-=a;
swap(a,b);
}
return ans;
}
};
|
提交记录
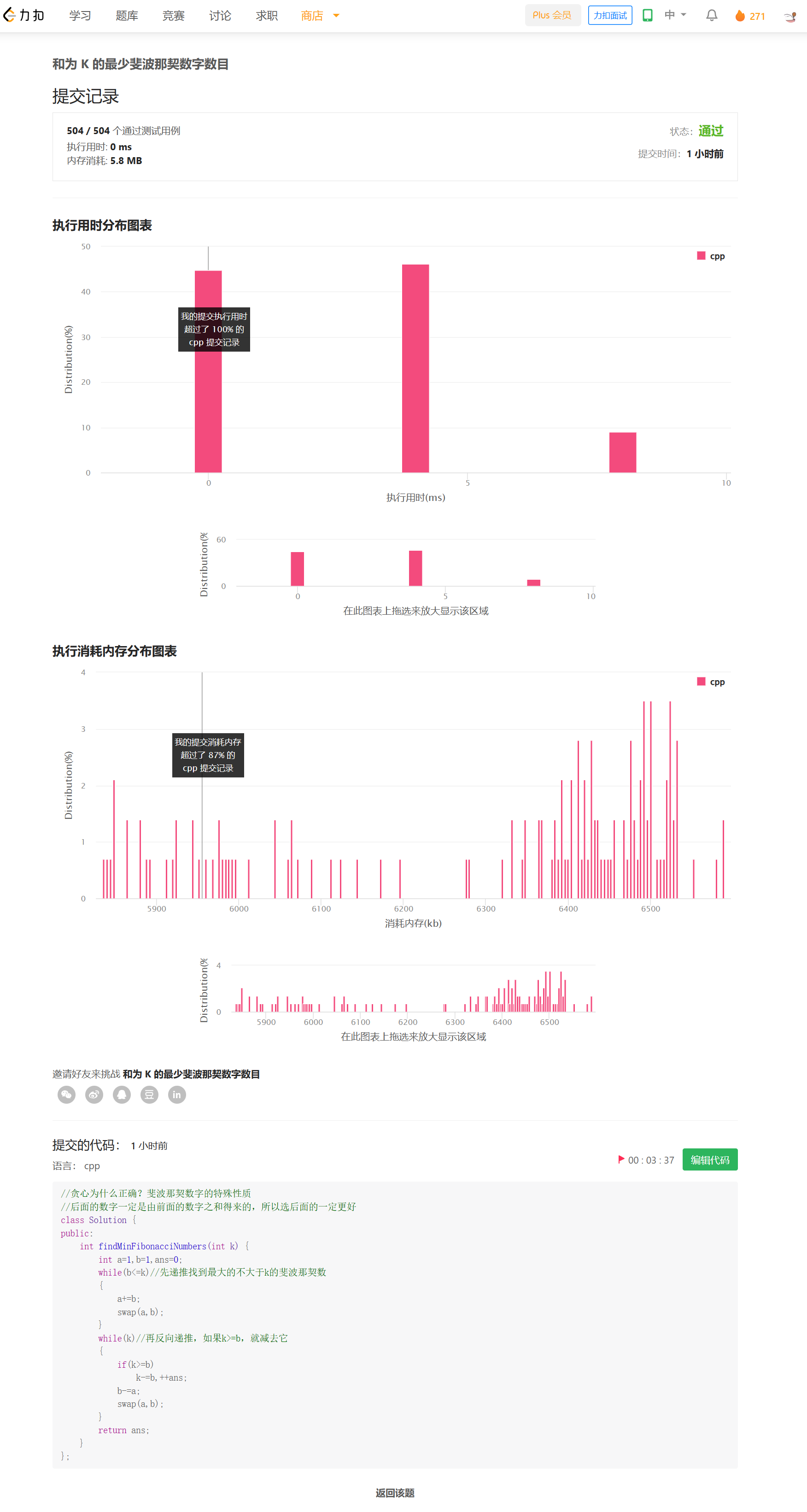
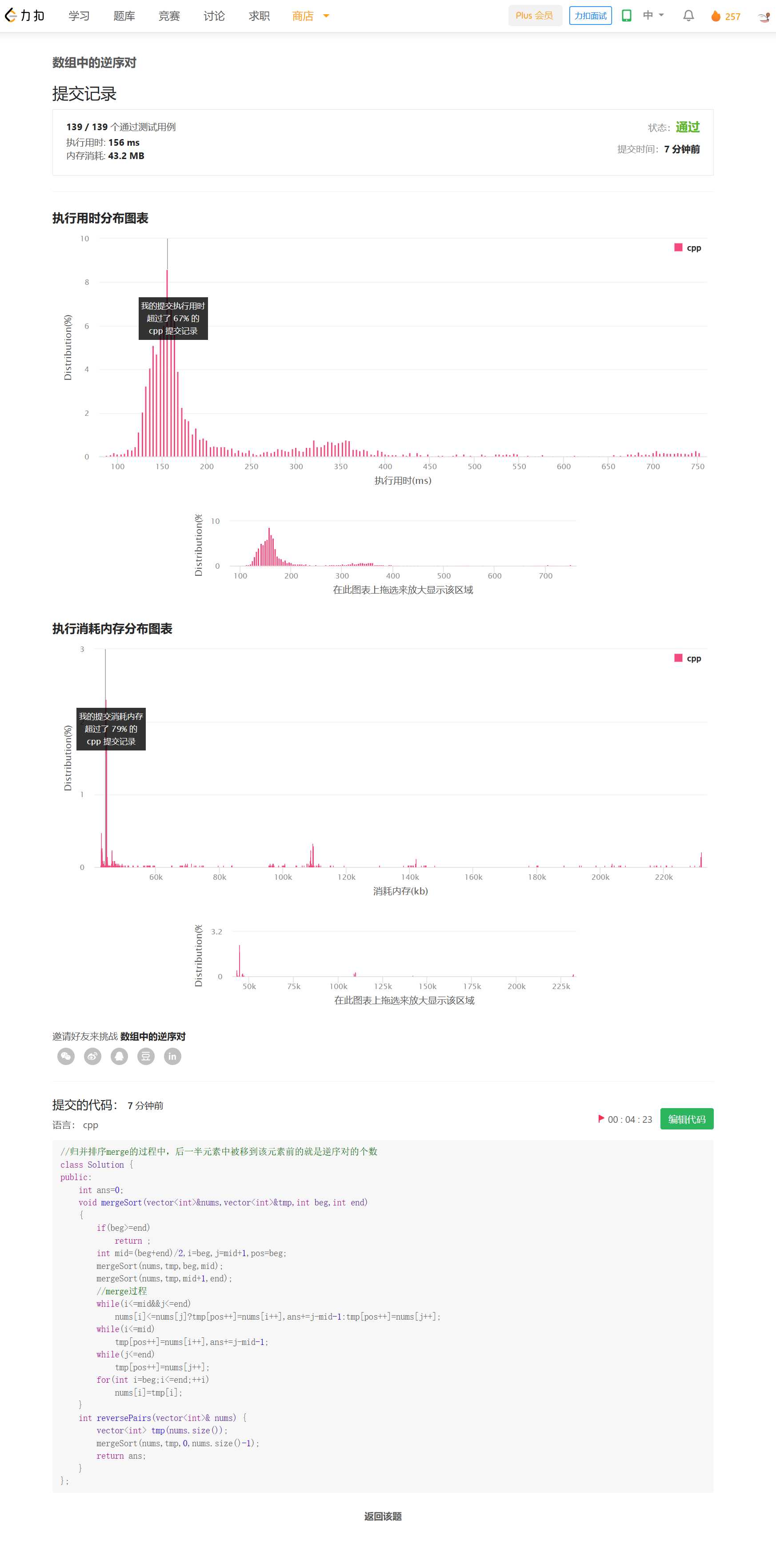
思路
进行归并排序,在merge的过程中,会合并前后两段使之有序。利用双指针i,j,则后一半中比nums[i]小的个数就是j-mid,这就是nums[i]在后一半中的逆序对数目。递归地进行这个过程,就可以得到全部的逆序对的数目。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public:
int ans=0;
void mergeSort(vector<int>&nums,vector<int>&tmp,int beg,int end)
{
if(beg>=end)
return ;
int mid=(beg+end)/2,i=beg,j=mid+1,pos=beg;
mergeSort(nums,tmp,beg,mid);
mergeSort(nums,tmp,mid+1,end);
while(i<=mid&&j<=end)
nums[i]<=nums[j]?tmp[pos++]=nums[i++],ans+=j-mid-1:tmp[pos++]=nums[j++];
while(i<=mid)
tmp[pos++]=nums[i++],ans+=j-mid-1;
while(j<=end)
tmp[pos++]=nums[j++];
for(int i=beg;i<=end;++i)
nums[i]=tmp[i];
}
int reversePairs(vector<int>& nums) {
vector<int> tmp(nums.size());
mergeSort(nums,tmp,0,nums.size()-1);
return ans;
}
};
|
提交记录