期末pre——回溯的剪枝策略
做题分析
因为很多算法还没学过,做得最多的困难题就是回溯和动态规划了,不过我也不太会动态规划,解决的方法通常是回溯+剪枝,在做题的过程中,我发现回溯+剪枝可以解决很多的动态规划问题,而且写起来比较容易
回溯介绍
回溯搜索是深度优先搜索(DFS)的一种,通俗地讲,回溯法采用的思想是“一直向下走,走不通就掉头”,类似于树的先序遍历。dfs和回溯法其主要的区别是:回溯法在求解过程中不保留完整的树结构,而深度优先搜索则记下完整的搜索树。
回溯的基本思想是:为了求得问题的解,先选择某一种可能的情况向前探索,在探索过程中,一旦发现原来的选择是错误的,就退回一步重新选择,继续向前探索,如此反复进行,直至得到解或证明无解
回溯是搜索算法中的一种控制策略。
未经剪枝的回溯将探索所有合理的解空间,因此复杂度也会比较高,比如N皇后问题的复杂度就达到了O(N!)
回溯的模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| 全局变量 ans
void solve(深度)
{
if(满足条件)
保存解
else
{
for(可以进行的操作)
{
保存结果
solve(深度+1)
回到原状态
}
}
}
|
什么时候用回溯?
由于回溯的复杂度很高,如果解空间的范围很大,则不适合用回溯法
如果要求我们找到全部的解或者解的数目(比如N皇后问题,全排列问题),很可能除了回溯法别无选择
但是,如果题目要求的是判断是否有解,或者寻找最优解,是否用回溯就要斟酌一下了,往往比较难的题目官方做法不是回溯,而是动态规划或者贪心,或是对字符串的特殊处理方法
但是,最优解/存在解问题能否用回溯解决呢?如果不考虑时间,一定是可以的(我都找到全部解了还能找不到最优解吗😂),但是如果真去硬做,基本上会收获一个TLE,不过,如果使用了适当的剪枝方法,回溯也是可以变得高效的,效率有时甚至可以超过动态规划,我下面主要想讲的就是如何剪枝
常用的剪枝方法
备忘录(记忆化搜索)
在搜索过程中,我们可能会进行很多重复的过程,请看下面这个我们都做过的题目——爬楼梯
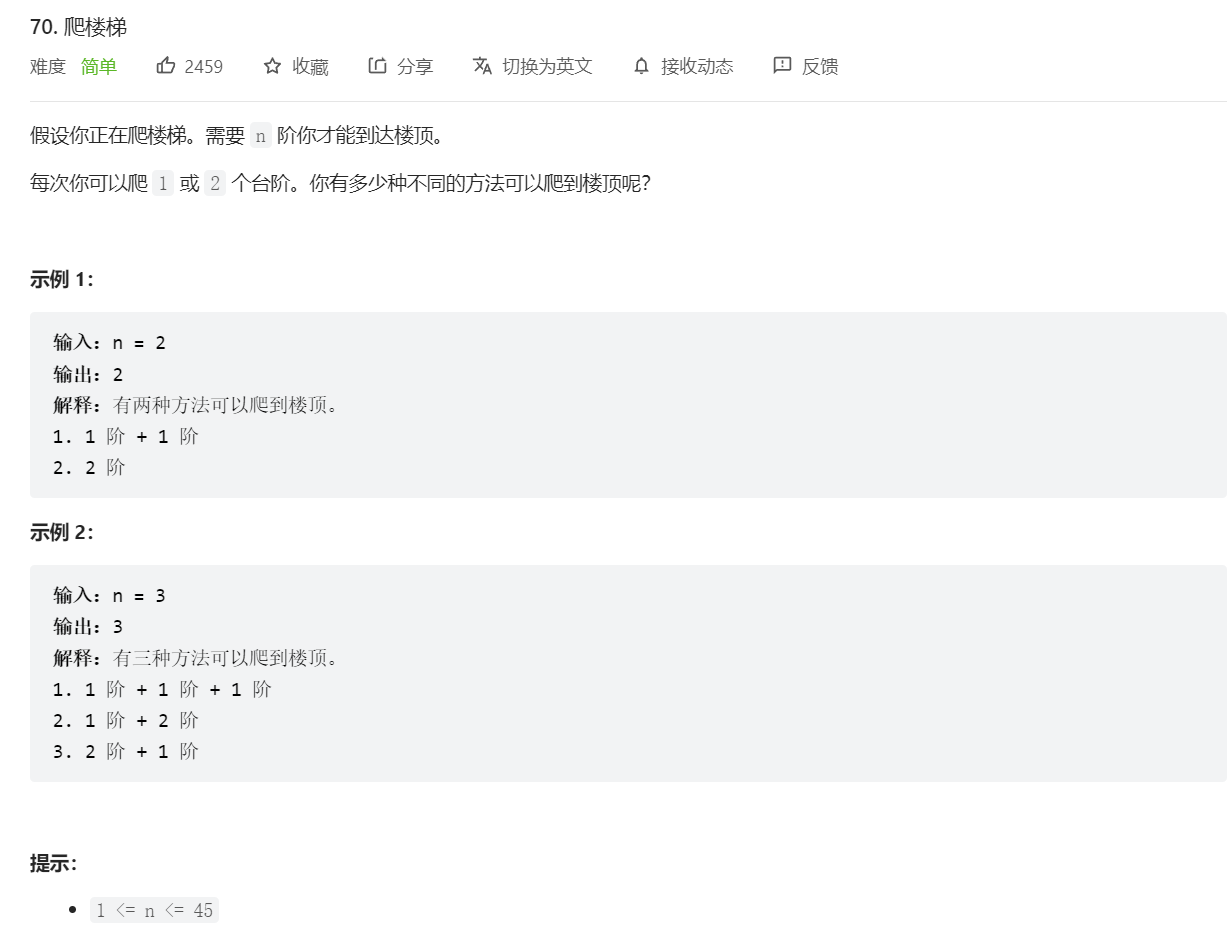
这个题目用一个简单的递归就可以解决——终止条件是只剩一层或两层台阶,否则方法数就是前两级台阶方法数之和
代码如下
1
2
3
4
5
6
| int climbStairs(int n) {
if(n==1||n==2)
return n;
else
return climbStairs(n-1)+climbStairs(n-2);
}
|
相信很多人就是这样写完就交了吧,结果超时了,为什么呢?其实是因为我们进行了大量的重复运算,比如,我们计算climbStairs(45)时,要计算climbStairs(44)和climbStairs(43),然后,计算climbStairs(44)时,又要计算climbStairs(43)和climbStairs(42),这里,climbStairs(43)就被重复计算了,如果我们用一个哈希表保存climbStairs(43)的值,需要时直接拿来用,不就不用再算一边了嘛
可以写出如下代码(用一个备忘录(memorandum)记录求过的值,需要值时先查表,如果有,直接用,否则计算并存入表中)
1
2
3
4
5
6
7
8
9
10
11
12
| unordered_map<int,int> memo;
int climbStairs(int n) {
if(memo.find(n)!=memo.end())
return memo[n];
if(n==1||n==2)
return n;
else
{
memo[n]=climbStairs(n-1)+climbStairs(n-2);
return memo[n];
}
}
|
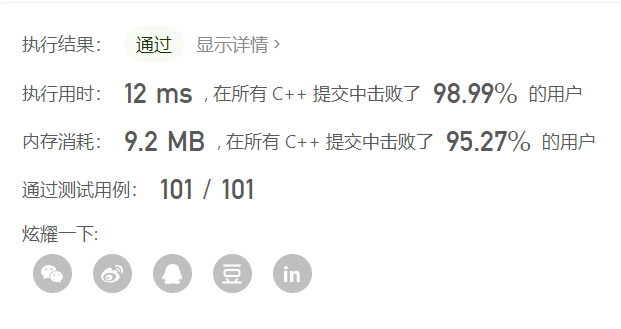
优化后,用时0ms
需要说明的是:本题仅仅是搜索,并不是回溯,举这道题只是为了引入备忘录这个剪枝方法(搜索过的节点以下的部分被剪掉了)
很多题目,在用了备忘录剪枝以后,就可以通过了(用时在1000ms以内),然而,这还和动态规划有很大差距,不过,如果抓住题目的特性来剪枝,效果能获得很大提升,下面来看两道困难题,以及它们是如何剪枝的
leetcode44——通配符匹配

这属于判断是否有解的类型,回溯中的”可以进行的操作”指的是*匹配的字符个数
如果熟悉之前的模板,很容易写出下面的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public:
bool ans=false;
void solve(string &s,string &p,int pos1,int pos2)
{
if(ans==true)
return ;
if(pos1==s.size()&&pos2==p.size())
ans=true;
else
{
while(pos1<s.size()&&pos2<p.size()&&(s[pos1]==p[pos2]||p[pos2]=='?'))
{
++pos1;
++pos2;
}
if(pos1==s.size()&&pos2==p.size())
ans=true;
else if(p[pos2]=='*')
{
int cnt=0;
while(pos1+cnt<=s.size())
solve(s,p,pos1+cnt++,pos2+1);
}
}
}
bool isMatch(string s, string p) {
solve(s,p,0,0);
return ans;
}
};
|
提交后发现超时了,毕竟题目要求的是是否有解,而不是找到所有解,用一般的回溯法自然会超时
根据上面的分析,可以知道,我们也进行了很多重复的搜索,所以可以加上哈希表的备忘录来去重,得到如下代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| class Solution {
public:
bool ans=false;
set<pair<int,int>> memo;
void solve(string &s,string &p,int pos1,int pos2)
{
if(memo.find(pair<int,int>{pos1,pos2})!=memo.end())
return ;
memo.insert({pos1,pos2});
if(ans==true)
return ;
if(pos1==s.size()&&pos2==p.size())
ans=true;
else
{
while(pos1<s.size()&&pos2<p.size()&&(s[pos1]==p[pos2]||p[pos2]=='?'))
{
++pos1;
++pos2;
}
if(pos1==s.size()&&pos2==p.size())
ans=true;
else if(p[pos2]=='*')
{
int cnt=0;
while(pos1+cnt<=s.size())
solve(s,p,pos1+cnt++,pos2+1);
}
}
}
bool isMatch(string s, string p) {
solve(s,p,0,0);
return ans;
}
};
|
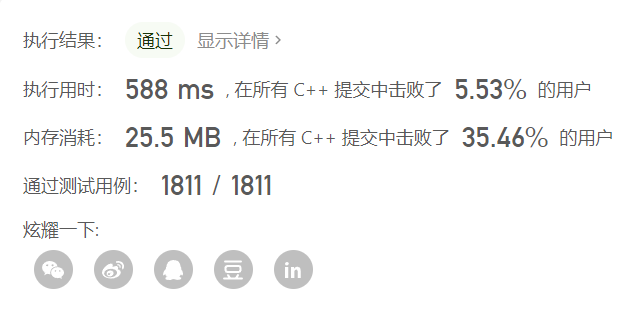
勉强过了,如果是周赛的话,就可以到此为止了,但还有优化的空间,这就要求我们根据题目本身来寻找剪枝策略
也就是我们要预先排除不合理的操作,使解空间尽量小,在本题中,考虑*的匹配什么时候是合理的
首先,对于连续的*,效果是一样的,可以视为一个,因此,对于连续的*,只考虑最后一个以缩小解空间
其次,对于s和p,如果能匹配成功,s至少要比p出去*的部分要长(因为*可以不匹配或是匹配多个,但是不能反向匹配,即不会变短),所以*匹配的长度应该使后面的部分有可能匹配成功,依照这两个条件,可以写出如下代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public:
bool ans=false;
int stars=0;
void solve(string &s,string &p,int pos1,int pos2)
{
if(ans==true)
return ;
if(pos1==s.size()&&pos2==p.size())
ans=true;
else
{
while(pos1<s.size()&&pos2<p.size()&&(s[pos1]==p[pos2]||p[pos2]=='?'))
{
++pos1;
++pos2;
}
if(pos1==s.size()&&pos2==p.size())
ans=true;
else if(p[pos2]=='*')
{
while(pos2<p.size()-1&&p[pos2+1]=='*')
{
--stars;
++pos2;
}
--stars;
int cnt=0;
while(s.size()-pos1-cnt+1>=p.size()-pos2-stars)
solve(s,p,pos1+cnt++,pos2+1);
}
}
}
bool isMatch(string s, string p) {
for_each(p.begin(),p.end(),[&](char &c){ if(c=='*') ++stars;});
solve(s,p,0,0);
return ans;
}
};
|
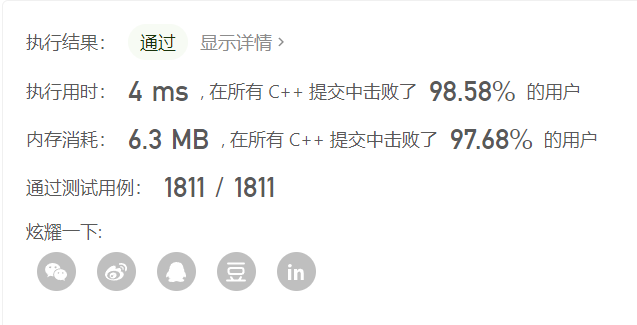
剪枝过后,接近击败双百
leetcode691——贴纸拼词
回溯思路:用一个remains表示剩下的需要寻找的字符串,一个num保存用的贴纸数,每一层查找尝试着用一张贴纸尽可能地找出remains中的字母
同时++num,如果num>=answer,说明不是最小贴纸数,停止搜索;如果remains==””,说明找到了,且num<answer,那么更新answer
关于剪枝:常规思路是每一次都遍历整个stickers,只要这个字符串中有target的字母就尝试搜索,也就是用first_of_all来判断
但实际上,我们可以人为地规定顺序,要求stickers[i]中必须有target[0]才查找,这对结果是无影响的
因为我们一定会需要有第一个字母的贴纸,所以先查找也无妨,但是效率影响是很大的
另外,用一个memo保存之前找到某个remains所用的最小num,如果现在的remains找过了且num>=记录值,终止搜索
(由于target.size()<=15,可知answer<=15||answer==-1,所以先假定answer==16,如果经历搜索仍为16,说明找不到)
代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public:
int answer=16;
int num=0;
unordered_map<string,int> memo;
void solve(vector<string> &stickers,string &remains)
{
if(remains=="")
answer=num;
if(num>=answer-1)
return ;
for(int i=0;i<stickers.size();++i)
{
if(stickers[i].find(remains[0])!=stickers[i].npos)
{
string temp=stickers[i],copy=remains;
int pos=0;
for(int j=0;j<remains.size();++j)
if((pos=temp.find(remains[j]))!=temp.npos)
{
temp.erase(pos,1);
remains.erase(j,1);
--j;
}
++num;
auto it=memo.find(remains);
if(it==memo.end()||it->second>num)
{
memo[remains]=num;
solve(stickers,remains);
}
remains=copy;
--num;
}
}
}
int minStickers(vector<string>& stickers, string target) {
solve(stickers,target);
return answer==16?-1:answer;
}
};
|
用时如下