leetcode 565. 数组嵌套
题目描述
索引从0开始长度为N的数组A,包含0到N - 1的所有整数。找到最大的集合S并返回其大小,其中 S[i] = {A[i], A[A[i]], A[A[A[i]]], ... }且遵守以下的规则。
假设选择索引为i的元素A[i]为S的第一个元素,S的下一个元素应该是A[A[i]],之后是A[A[A[i]]]... 以此类推,不断添加直到S出现重复的元素。
示例 1:
输入: A = [5,4,0,3,1,6,2]
输出: 4
解释:
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.
其中一种最长的 S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}
提示:
N是[1, 20,000]之间的整数。A中不含有重复的元素。A中的元素大小在[0, N-1]之间。
题解——作图帮助理解
通过作图来理解题意
题意可以描述成不断地执行i=A[i],每次取出A[i],直到出现重复,显然,这会形成循环,下面通过对样例的作图来帮助大家理解一下。
根据题目的描述,题目的例子可以这样作出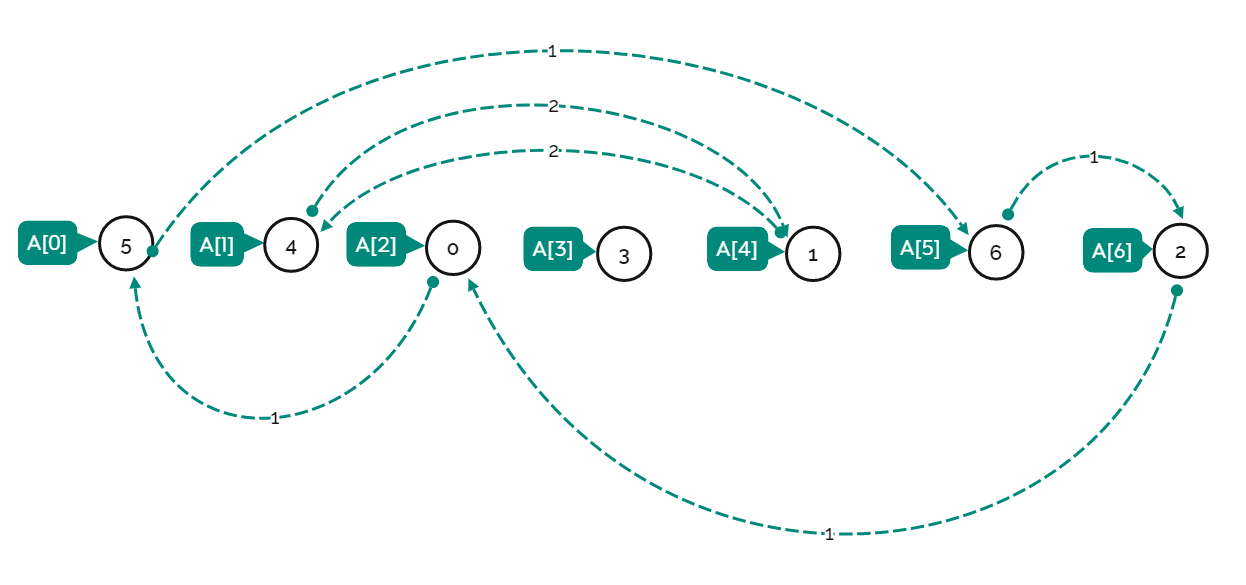
循环1:A[5]=6,A[6]=2,A[2]=0,A[0]=5,循环2:A[4]=1,A[1]=4,循环3(自循环):A[3]=3
共三组循环,可以把它们拆分开来,变成下图的样子
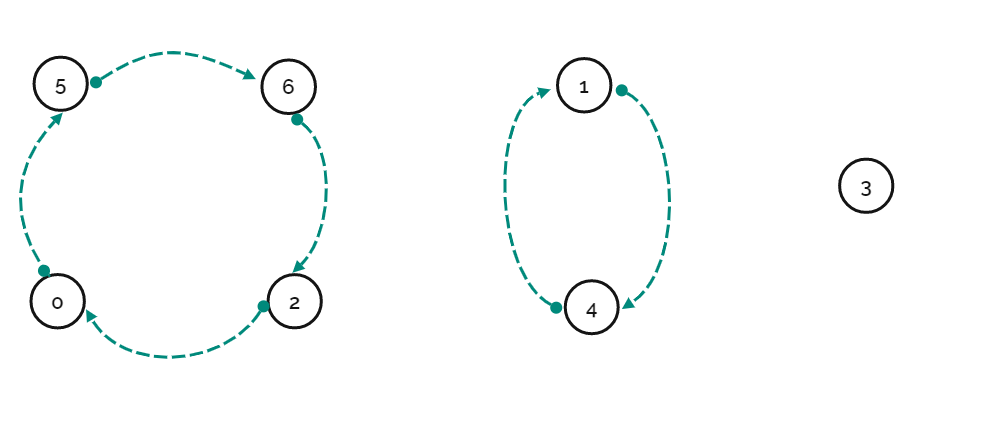
可以总结出一些性质
- 对每一个循环,无论从哪里进入,结果都是一样的,这是很直观的
- 由于不存在重复数字,也就是说不可能两个数字指向同一个地方,所以每个循环不存在交叉,因此查找过的元素一定不会被再次查找
依据上面的性质,我们解题的思路如下
按照题意模拟,顺序遍历整个数组,尝试以它为开头找到循环,对于我们经过的每一个元素,首先,不应再用它当开头——这会造成重复查找;其次,其他循环不会经过它——因为没有交叉。也就是说,我们一旦经过某个元素,以后就不可能再用上它,所以可以把它抹去,可以原地地将它置为-1,或者是n等等不会出现的数。
不断查找,直到回到开头,这个循环结束,sz记录了循环的长度。返回最大的sz即可
可以写出如下代码,用时100ms左右
1 | class Solution { |
7.18更新
看到评论区有人问为什么一定在入口处成环,确实有点绕,在这里具体解释一下,希望能帮助理解。
分为两部分证明:
- 先证明一定成环
其实根据题意这是直观的,如果不理解,可以这么想:在没有回头指向遍历过的节点时,这个结构是线性的,但是最终状态不可能是线性的,因为每个节点都必然指向某个节点,也必然被某个节点所指,所以它不可能真正地有头有尾。最长的可能就是遍历完整个数组,最后返回到某个值并成环。
- 接下来证明必然在遍历开始处成环
关键点在于没有相同元素。根据上面的证明,一定成环,假如不在开头处成环,就一定返回到中间某个节点,但是这必然造成重复。何以见得?首先,在遍历时,已经有一个元素指向它了,现在又返回到它,不就有两个相同的值了吗?类似于下图的情况。所以必须返回到还没有被指向的节点,也就是遍历的开头。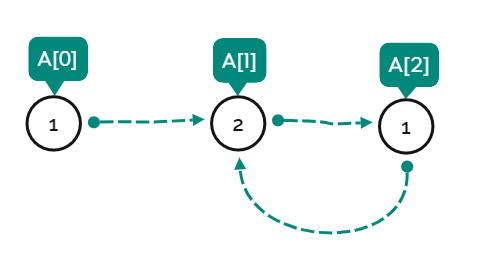
所以,我们就证明了,每次遍历必然成环,且成环处一定是开头。





