leetcode 2360. 图中的最长环

题目描述

给你一个 n 个节点的 有向图 ，节点编号为 0 到 n - 1 ，其中每个节点至多有一条出边。

图用一个大小为 n 下标从 0 开始的数组 edges 表示，节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边，那么 edges[i] == -1 。

请你返回图中的最长环，如果没有任何环，请返回 -1 。

一个环指的是起点和终点是 同一个 节点的路径。

示例 1：

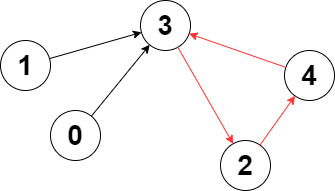
输入：edges = [3,3,4,2,3]
输出去：3
解释：图中的最长环是：2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ，所以返回 3 。

示例 2：

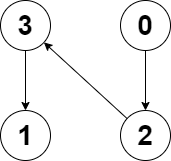
输入：edges = [2,-1,3,1]
输出：-1
解释：图中没有任何环。

提示：

n == edges.length
2 <= n <= 10⁵
-1 <= edges[i] < n
edges[i] != i

题解——板子题

这道题和7.17的每日一题十分相似，也就是565.数组嵌套，都是寻找图中最大环的问题。这也是一类图论板子题。不同点就是这道题的入度和出度是不定的，但是保证了出度最多为1。如果没做过这类题，推荐先去做一下那题。

思路

首先想想一个节点在环中的条件，它必须被环中节点指向，并指向环中节点。最多有一条出边，就保证了它不可能指向两个节点，也就不可能同时处在两个环中。所以对于每一个节点，要么不在环中，要么就在一个环中，这是很重要的点。
正因如此，我们遍历过的节点不必再次用到了。因为如果这条路径上有环，不论从哪个节点出发(环上或环外)，都一定会遍历整个环，而且只会遍历这一个环(无交叉)。而如果这条路径上没有环，哪个节点出发都不可能有环。所以遍历过的节点可以大胆地置为-1，表示不再使用。
在遍历的过程中，我们记录遍历的长度和各个节点离开头的距离，当回到遍历过的节点时，中止，环的长度就是整个长度减去该节点与起点间的距离。

代码

class Solution {
public:
    int longestCycle(vector<int>& edges) {
        int ans=-1;
        for(int i=0;i<edges.size();++i)//顺序遍历节点，尝试以它为开头
        {
            unordered_map<int,int> length;//记录距离起点的长度
            if(edges[i]==-1)//之前找过的地方或者终点，跳过！
                continue;
            int next=edges[i],size=1; //用next记录下一个查找的位置，size记录循环长度
            while(length.find(next)==length.end()&&next!=-1)//如果没有出现重复，继续
            {
                int temp=edges[next];//记录下一个跳转的位置
                edges[next]=-1;//赋为-1，标记为查找过
                length[next]=size;//记录距离
                ++size;
                next=temp;//改变next为下一跳
            }
            if(next!=-1)//如果确实是因为找到了环结束的，更新ans
                ans=max(ans,size-length[next]);
        }
        return ans;
    }
};