期末编程报告

第一次作业第6题

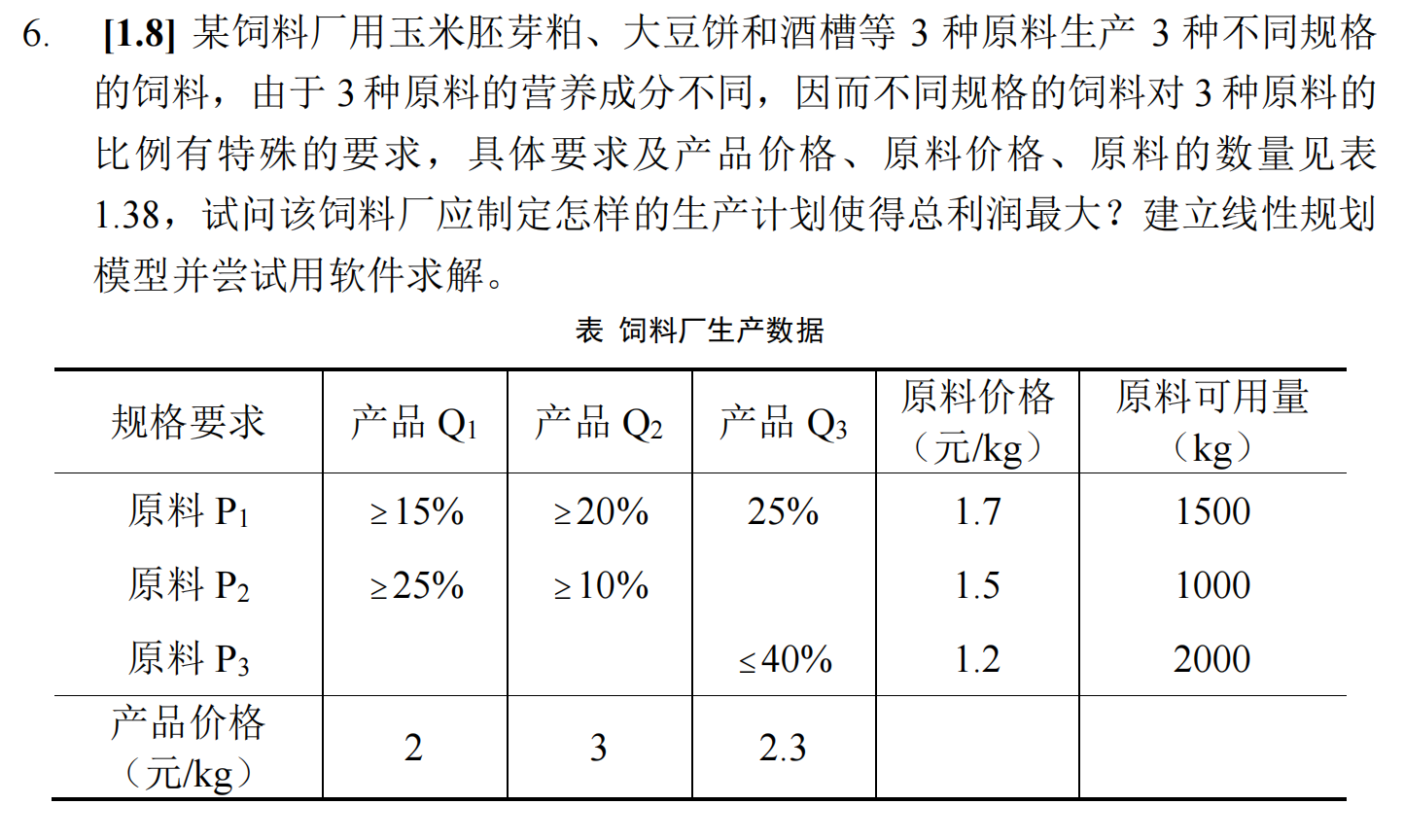
OR-HW1-T6

建模

设为产品中原料的含量，线性规划模型如下：

用MATLAB求解

代码如下（脚本见HW1_T6.m）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
%目标函数系数向量
f=[0.3 0.5 0.8 1.3 1.5 1.8 0.6 0.8 1.1];
%不等式约束左端矩阵
A=[ 1 0 0 1 0 0 1 0 0
    0 1 0 0 1 0 0 1 0
    0 0 1 0 0 1 0 0 1
    -0.85 0.15 0.15 0 0 0 0 0 0
    0.2 -0.8 0.2 0 0 0 0 0 0
    0 0 0 -0.75 0.25 0.25 0 0 0
    0 0 0 0.1 -0.9 0.1 0 0 0
    0 0 0 0 0 0 0.4 0.4 -0.6];
%不等式约束右端向量
b=[1500 1000 2000 0 0 0 0 0];
%等式约束左端矩阵
Aeq=[0.25 0.25 -0.75 0 0 0 0 0 0];
%等式约束右端向量
beq=0;
%下界和上界
lb=[0 0 0 0 0 0 0 0 0];
ub=[inf inf inf inf inf inf inf inf inf];
%调用linprog线性规划函数进行求解
[x,fval]=linprog(-f,A,b,Aeq,beq,lb,ub)

求解结果为，也就是只生产产品将使利润最大。

第三次作业第1题

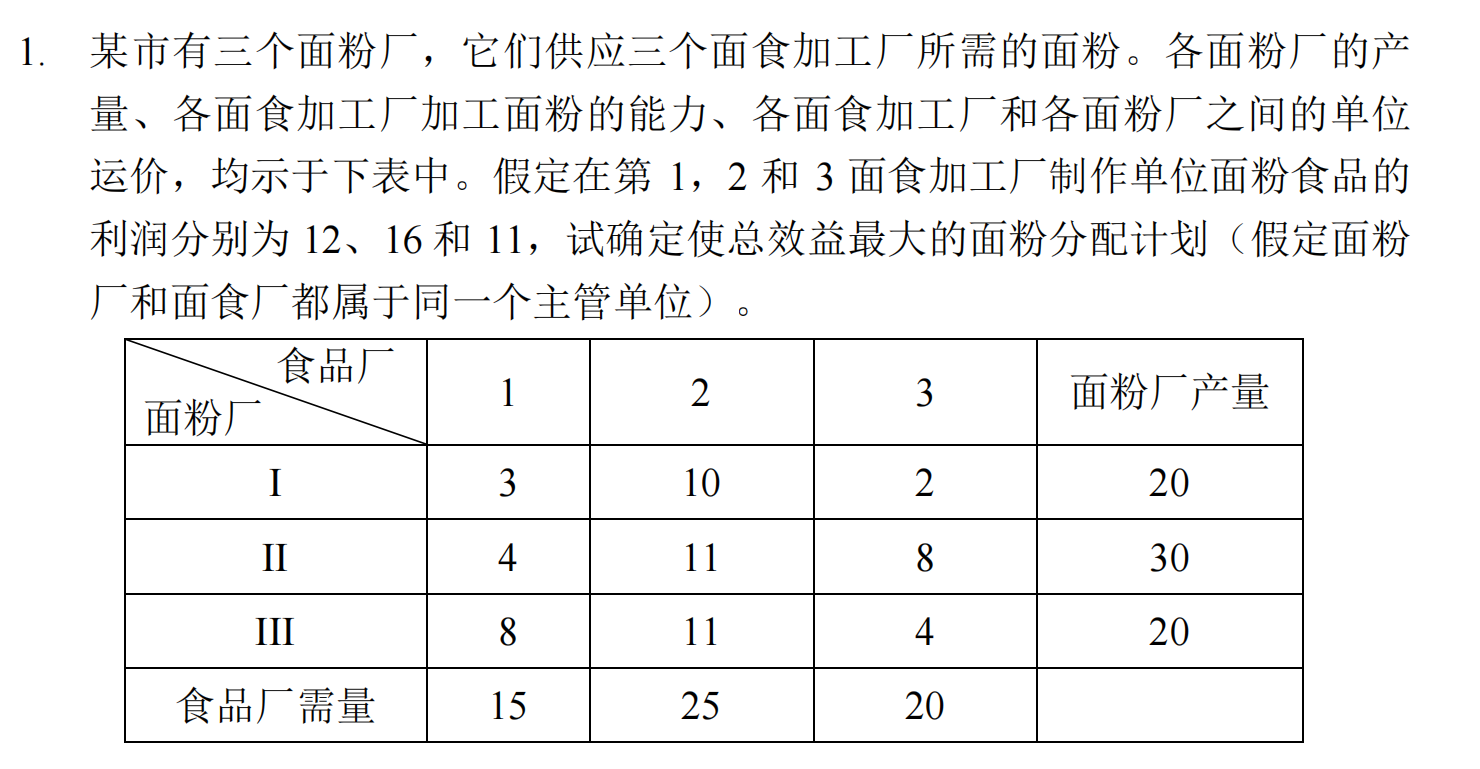
image-20230102154445184

建模

该问题为一个产大于销的运输问题，所以要虚拟一个食品厂，到它的运费均为0。

同时，我们的目标是最大化效益，而效益=利润-运费，由于每个食品厂的需求都将被满足，所以利润是确定的，只需要找到最小运价，就能得到最大效益。运价表如下：

1 2 3 D 产
I 3 10 2 0 20
II 4 11 8 0 30
III 8 11 4 0 20
需 15 25 20 10

为了用MATLAB求解，将运输问题转化为线性规划问题。建模如下：

用MATLAB求解

代码如下（脚本见HW3_T1.m）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
%目标函数系数向量
f=[3 10 2 0 4 11 8 0 8 11 4 0];
%等式约束左端矩阵
Aeq=[1 1 1 1 0 0 0 0 0 0 0 0
     0 0 0 0 1 1 1 1 0 0 0 0
     0 0 0 0 0 0 0 0 1 1 1 1
     1 0 0 0 1 0 0 0 1 0 0 0
     0 1 0 0 0 1 0 0 0 1 0 0
     0 0 1 0 0 0 1 0 0 0 1 0
     0 0 0 1 0 0 0 1 0 0 0 1];
%等式约束右端向量
beq=[20 30 20 15 25 20 10];
%下界和上界
lb=[0 0 0 0 0 0 0 0 0 0 0 0];
ub=[inf inf inf inf inf inf inf inf inf inf inf inf];
%调用linprog线性规划函数进行求解
[x,fval]=linprog(f,[],[],Aeq,beq,lb,ub)

求得结果为，最小运费为375，又知利润为，故最大效益为，一种使效益最大的运输方案为

第四次作业第4题

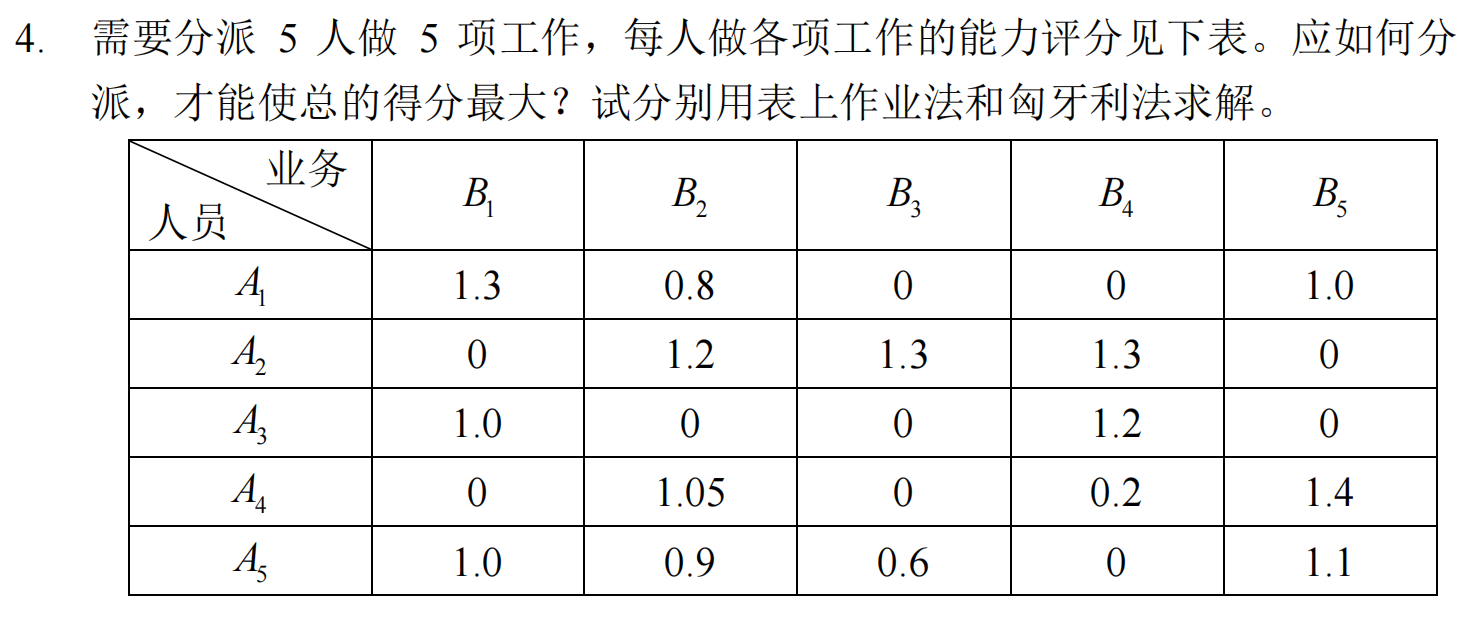
image-20230102161747401

建模

这是一个指派问题，建立0-1整数规划模型如下：

用MATLAB求解

代码如下（脚本见HW4_T4.m）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
%目标函数系数向量
f=[1.3 0.8 0 0 1.0 0 1.2 1.3 1.3 0 1.0 0 0 1.2 0 0 1.05 0 0.2 1.4 1.0 0.9 0.6 0 1.1];
%等式约束左端矩阵
Aeq=[1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
     0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
     0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
     0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0
     0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1
     1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0
     0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0
     0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0
     0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0
     0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1];
%等式约束右端向量
beq=[1 1 1 1 1 1 1 1 1 1];
%必须为整数的变量
intcon=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25];
%下界和上界
lb=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];
ub=[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1];
%调用intlinprog整数规划函数进行求解
[x,fval]=intlinprog(-f,intcon,[],[],Aeq,beq,lb,ub)

求解结果如下

也即最佳指派方案为：，最大得分6.1