leetcode 712. 两个字符串的最小ASCII删除和
题目描述leetcode712. 两个字符串的最小ASCII删除和
给定两个字符串s1 和 s2,返回 使两个字符串相等所需删除字符的 ASCII 值的最小和 。
示例 1:
输入: s1 = "sea", s2 = "eat"
输出: 231
解释: 在 "sea" 中删除 "s" 并将 "s" 的值(115)加入总和。
在 "eat" 中删除 "t" 并将 116 加入总和。
结束时,两个字符串相等,115 + 116 = 231 就是符合条件的最小和。
示例 2:
输入: s1 = "delete", s2 = "leet"
输出: 403
解释: 在 "delete" 中删除 "dee" 字符串变成 "let",
将 100[d]+101[e]+101[e] 加入总和。在 "leet" 中删除 "e" 将 101[e] 加入总和。
结束时,两个字符串都等于 "let",结果即为 100+101+101+101 = 403 。
如果改为将两个字符串转换为 "lee" 或 "eet",我们会得到 ...
leetcode 2360. 图中的最长环
题目描述leetcode2360. 图中的最长环
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示,节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边,那么 edges[i] == -1 。
请你返回图中的 最长 环,如果没有任何环,请返回 -1 。
一个环指的是起点和终点是 同一个 节点的路径。
示例 1:
输入:edges = [3,3,4,2,3]
输出去:3
解释:图中的最长环是:2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ,所以返回 3 。
示例 2:
输入:edges = [2,-1,3,1]
输出:-1
解释:图中没有任何环。
&nb ...
leetcode 2350. 不可能得到的最短骰子序列
题目描述leetcode2350. 不可能得到的最短骰子序列
给你一个长度为 n 的整数数组 rolls 和一个整数 k 。你扔一个 k 面的骰子 n 次,骰子的每个面分别是 1 到 k ,其中第 i 次扔得到的数字是 rolls[i] 。
请你返回 无法 从 rolls 中得到的 最短 骰子子序列的长度。
扔一个 k 面的骰子 len 次得到的是一个长度为 len 的 骰子子序列 。
注意 ,子序列只需要保持在原数组中的顺序,不需要连续。
示例 1:
输入:rolls = [4,2,1,2,3,3,2,4,1], k = 4
输出:3
解释:所有长度为 1 的骰子子序列 [1] ,[2] ,[3] ,[4] 都可以从原数组中得到。
所有长度为 2 的骰子子序列 [1, 1] ,[1, 2] ,... ,[4, 4] 都可以 ...
leetcode 565. 数组嵌套
题目描述leetcode565. 数组嵌套
索引从0开始长度为N的数组A,包含0到N - 1的所有整数。找到最大的集合S并返回其大小,其中 S[i] = {A[i], A[A[i]], A[A[A[i]]], ... }且遵守以下的规则。
假设选择索引为i的元素A[i]为S的第一个元素,S的下一个元素应该是A[A[i]],之后是A[A[A[i]]]... 以此类推,不断添加直到S出现重复的元素。
示例 1:
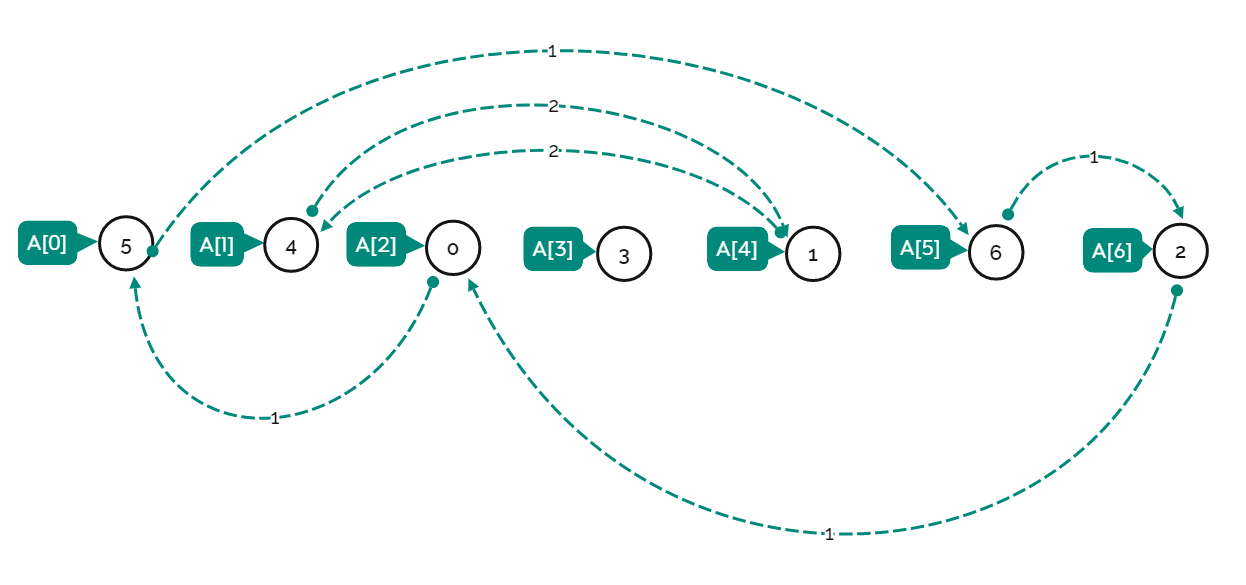
输入: A = [5,4,0,3,1,6,2]
输出: 4
解释:
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.
其中一种最长的 S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}
提示:
N是[1, 20,000]之间的整数。
A中不含有重复的元素。
A中的元素大小在[0, N-1]之间。
题解——作图帮助理解通过作图来理解题 ...
leetcode 2333. 最小差值平方和
题目描述leetcode2333. 最小差值平方和
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,长度为 n 。
数组 nums1 和 nums2 的 差值平方和 定义为所有满足 0 <= i < n 的 (nums1[i] - nums2[i])2 之和。
同时给你两个正整数 k1 和 k2 。你可以将 nums1 中的任意元素 +1 或者 -1 至多 k1 次。类似的,你可以将 nums2 中的任意元素 +1 或者 -1 至多 k2 次。
请你返回修改数组 nums1 至多 k1 次且修改数组 nums2 至多 k2 次后的最小 差值平方和 。
注意 ...
leetcode 648. 单词替换
题目描述leetcode648. 单词替换
在英语中,我们有一个叫做 词根(root) 的概念,可以词根后面添加其他一些词组成另一个较长的单词——我们称这个词为 继承词(successor)。例如,词根an,跟随着单词 other(其他),可以形成新的单词 another(另一个)。
现在,给定一个由许多词根组成的词典 dictionary 和一个用空格分隔单词形成的句子 sentence。你需要将句子中的所有继承词用词根替换掉。如果继承词有许多可以形成它的词根,则用最短的词根替换它。
你需要输出替换之后的句子。
示例 1:
输入:dictionary = ["cat","bat","rat"], sentence = "the cattle was rattled by the battery"
输出:"the cat was rat by the bat"
示例 2:
输入:dictionary = ["a","b","c"], sentence = "aadsfasf absbs bbab cadsfafs"
...
leetcode 241. 为运算表达式设计优先级
题目描述leetcode241. 为运算表达式设计优先级
给你一个由数字和运算符组成的字符串 expression ,按不同优先级组合数字和运算符,计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。
生成的测试用例满足其对应输出值符合 32 位整数范围,不同结果的数量不超过 104 。
示例 1:
输入:expression = "2-1-1"
输出:[0,2]
解释:
((2-1)-1) = 0
(2-(1-1)) = 2
示例 2:
输入:expression = "2*3-4*5"
输出:[-34,-14,-10,-10,10]
解释:
(2*(3-(4*5))) = -34
((2*3)-(4*5)) = -14
((2*(3-4))*5) = -10
(2*((3-4)*5)) = -10
(((2*3)-4)*5) = 10
提示:
1 <= expression.length <= 20
expression 由数字和算符 '+'、'-' 和 '*' 组成。
...
leetcode 2321. 拼接数组的最大分数
题目描述leetcode2321. 拼接数组的最大分数
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,长度都是 n 。
你可以选择两个整数 left 和 right ,其中 0 <= left <= right < n ,接着 交换 两个子数组 nums1[left...right] 和 nums2[left...right] 。
例如,设 nums1 = [1,2,3,4,5] 和 nums2 = [11,12,13,14,15] ,整数选择 left = 1 和 right = 2,那么 nums1 会变为 [1,12,13,4,5] 而 nums2 会变为 [11,2,3,14,15] 。
你可以选择执行上述操作 一次 或不执行任何操作。
数组的 分数 取 sum(nums1) 和 sum(nums2) 中的最大值,其中 sum(arr) 是数组 arr 中所有元素之和。
返回 可能的最大分数 。
子数组 是数组中连续的一个元素序列。arr[left...right] 表示子数组包含 nums 中下标 left 和 r ...
leetcode 2320. 统计放置房子的方式数
题目描述2320. 统计放置房子的方式数
一条街道上共有 n * 2 个 地块 ,街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n 编号。每个地块上都可以放置一所房子。
现要求街道同一侧不能存在两所房子相邻的情况,请你计算并返回放置房屋的方式数目。由于答案可能很大,需要对 109 + 7 取余后再返回。
注意,如果一所房子放置在这条街某一侧上的第 i 个地块,不影响在另一侧的第 i 个地块放置房子。
示例 1:
输入:n = 1
输出:4
解释:
可能的放置方式:
1. 所有地块都不放置房子。
2. 一所房子放在街道的某一侧。
3. 一所房子放在街道的另一侧。
4. 放置两所房子,街道两侧各放置一所。
示例 2:
输入:n = 2
输出:9
解释:如上图所示,共有 9 种可能的放置方式。
提示:
1 <= n <= 104
题解——找规律+递推
思路类似于上台阶,找到递推关系即可
记录上一个位置放置和不放置的方法数,不相临可以解释为上一个位置不放,这一个位置才能放,所以下一个位置放置的方法数就是上 ...
leetcode 2311. 小于等于 K 的最长二进制子序列
题目描述leetcode2311. 小于等于 K 的最长二进制子序列
给你一个二进制字符串 s 和一个正整数 k 。
请你返回 s 的 最长 子序列,且该子序列对应的 二进制 数字小于等于 k 。
注意:
子序列可以有 前导 0 。
空字符串视为 0 。
子序列 是指从一个字符串中删除零个或者多个字符后,不改变顺序得到的剩余字符序列。
示例 1:
输入:s = "1001010", k = 5
输出:5
解释:s 中小于等于 5 的最长子序列是 "00010" ,对应的十进制数字是 2 。
注意 "00100" 和 "00101" 也是可行的最长子序列,十进制分别对应 4 和 5 。
最长子序列的长度为 5 ,所以返回 5 。
示例 2:
输入:s = "00101001", k = 1
输出:6
解释:"000001" 是 s 中小于等于 1 的最长子序列,对应的十进制数字是 1 。
最长子序列的长度为 6 ...