树与森林

上周学习了二叉树，这是一种比较特殊的树，因为它至多只有两个孩子。而实际上，一般的树可以有多个孩子，这就使问题变得复杂了。首先要解决的是，如何表示一颗一般树？大致有双亲表示法、孩子链表法、孩子兄弟法三种。

树的三种表示方法

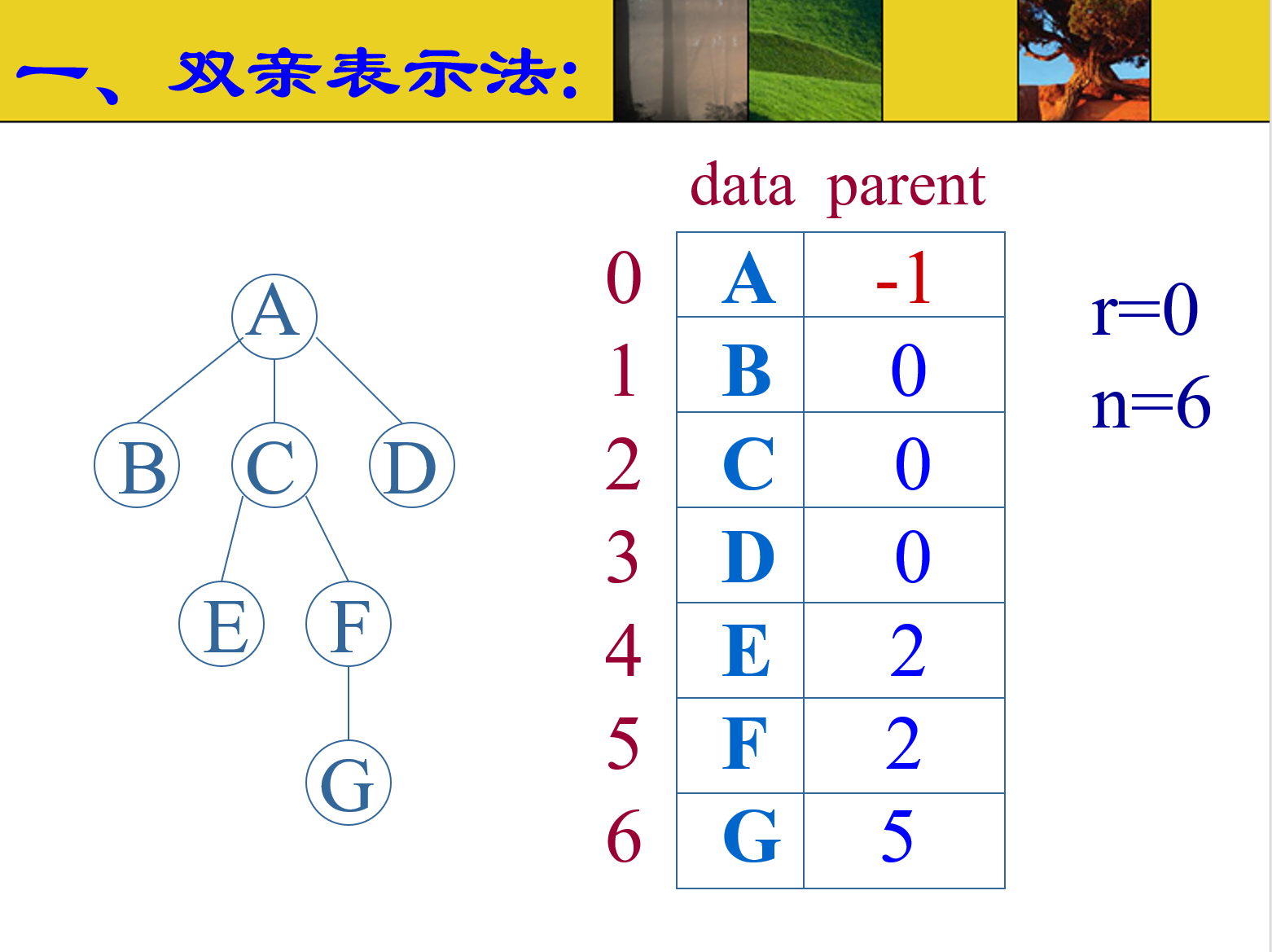
双亲表示法

顾名思义，就是给每个节点添加一个数据域，存放它的双亲的信息(说是双亲，其实只有一个)。这样的储存方法，给定一个节点，我们可以用O(1)的时间找到父亲，但却要遍历整颗树来找齐它的孩子。同时，由于没有自上而下的指针，我们至少要保存全部的叶节点，而现实中，是保存了全部的节点，并保存在一张表中。如图所示。

image-20221111223935523

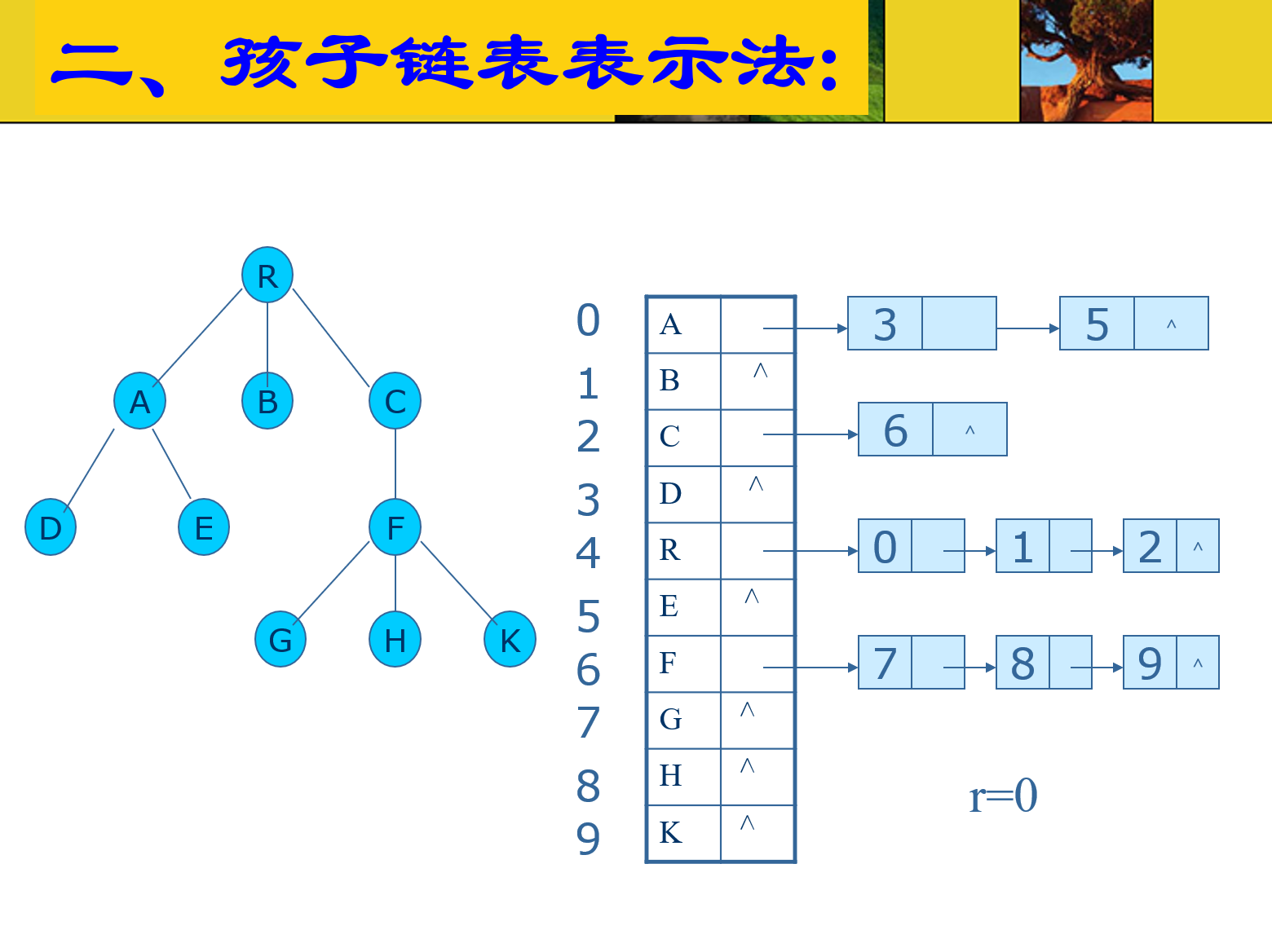
孩子链表表示法

回顾二叉树的表示方法，我们是通过两个指针left和right来指示两个孩子，能否用在一般树中呢？有一个困难是：我们不知道每个节点可能有多少个孩子。所以，可以用一个vector<TreeNode*>来保存孩子指针们。不过，由于树结构可能面临频繁的增删，应该用链表代替数组，也就是list<TreeNode*>来保存孩子。如图所示。这种方法，我们只要保存根节点即可。

此外，如果知道了最大分叉数，就可以直接写成数组了，比如字典树，由于一共只有26个英文字母，所以用的是Trie* children[26]储存孩子节点们。

image-20221111224644834

孩子兄弟表示法

对于树上的每一个节点，我们用一个二叉树节点代替它，将left(firstChild)指向它的第一个孩子，right(nextsibling)指向它的紧邻的兄弟。通过这样的转化，我们可以将任意一颗树转化为二叉树。因此，之前对二叉树的操作又可以移植过来了。孩子兄弟表示法可以作为将普通树转化为二叉树的最有效方法，通常又被称为”二叉树表示法”或”二叉链表表示法”。如图所示

image-20221111230959421

树的遍历

树共有三种遍历方法：先根遍历、后根遍历和层序遍历。先根遍历是先访问根节点，然后依次从左到右访问每一棵子树；后根遍历是先依次访问每一颗子树，再访问根节点；层序遍历是从上往下、从左往右访问每一个节点。与二叉树相比，树并没有中根遍历。这是因为每个节点孩子数不确定，不好说访问几颗子树后访问根节点，所以没有定义中根遍历。

树与对应二叉树遍历的联系

先看一个例子：

image-20221112011648535

树的先根遍历：ABEKFCGDHIJ，后根遍历：KEFBGCHIJDA，层序遍历：ABCDEFGHIJK

二叉树的先序遍历：ABEKFCGDHIJ，中序遍历：KEFBGCHIJDA，后序遍历：KFEGJIHDCBA，层序遍历：ABECKFGDHIJ

可以直观地看出，树的先根遍历对应二叉树的先序遍历；树的后根遍历对应二叉树的中序遍历。下面证明之：

  • 对先根遍历，树的遍历是这样进行的：先访问根节点，然后visit along first branch，并立即访问，直到找到没有子树的节点，向上找到有第二颗子树的节点，将控制权转交给它的下一棵子树，访问过后，逐级往上。而对应二叉树是这样进行的：访问根节点，然后visit along left branch，并随即访问，这相当于上面的visit along first branch，因为左孩子对应第一棵子树。直到找到没有左子树的节点，将控制权转交给它的右子树，也就是next sibling，这相当于上面的找到下一棵子树，接着逐级往上。所以先根遍历等价于先序遍历。
  • 对后根遍历，树的遍历是这样进行的：visit along first branch并找到没有子树的节点，访问之，然后访问它的下一个兄弟，待所有子树访问完后，再访问父亲，逐级往上。而对应二叉树的中序遍历是这样进行的：visit along left branch直到找到没有左子树的节点，访问之，然后控制权移交给它的右子树，相当于它的下一个兄弟。待它的子孙都访问完了，访问它的父亲，然后再访问父亲的兄弟们，逐级往上。所以后根遍历等价于中序遍历。

那树的层序遍历相当于二叉树的什么呢？其实是二叉树逆时针旋转45度再进行层序遍历的结果。体现在代码上，就是对每一个节点的左孩子，visit along right branch，并将沿途节点入队即可。

森林

森林，顾名思义，就是多棵树的组合。森林也可以转化为二叉树，方法是构建一个虚拟根节点，将各棵树的根节点作为它的孩子们，形成一整棵树，接着转为二叉树，再把根节点删掉即可。

再遍历森林时，我们将它分为三部分：根节点，第一棵子树和其他子树。森林有两种遍历方法：先序遍历和中序遍历，它们等价于对形成的二叉树进行先序和后序遍历，这里就不证明了。

练习题

这周有两道题目，第一题是将双亲表示法表示的树转换成孩子兄弟法表示的二叉树，思路就是如果出现过兄弟了，就将当前节点作为上一个兄弟的右子树，否则作为父亲的左子树，没什么好说的。

第二道题有点意思，给定一颗用孩子兄弟法表示的树，如何求出原森林的深度？求深度，一种很直白的方法就是层序遍历，这就回到了上面那个问题，即树的层序遍历如何体现在二叉树上?上面讨论过了，这里给出代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int getDepthOfForest(TreeNode *root)
{
    int depth = 0;
    queue<TreeNode *> q;
    while (root)//visitAlongRightBranch
    {
        q.push(root);
        root = root->right;
    }
    while (!q.empty()) 
    {
        ++depth;
        int cnt = q.size();            
        for (int i = 1; i <= cnt; ++i) 
        {
            TreeNode *node = q.front()->left;
            q.pop();
            while (node)//visitAlongRightBranch
            {
                q.push(node);
                node = node->right;
            }
        }
    }
    return depth;
}

事实上，如果仅仅需要得到深度，不用这么麻烦。我们只要对二叉树进行后序遍历，向上返回从该节点开始右下方的最大深度即可，也就是孩子的深度+1与兄弟深度中较大者，也就是max(leftDepth+1,rightDepth)。代码如下：

1
2
3
4
5
6
int getDepth(TreeNode *node)
{
    if (node == NULL)
        return 0;
    return max(getDepth(node->left) + 1, getDepth(node->right));
}