广义表的深度
广义表的定义
本周的数据结构与算法继续学习数组和广义表。主要讲了广义表。广义表是一种比较抽象的数据结构,它包含两个部分:原子和表。相较于链表和容器而言,它的元素不止一种,而且由于表可以嵌套,一张广义表是递归定义的。广义表主要应用于LISP语言(实际上LISP语言也只有广义表)。
广义表的表示
通常,表用大写字母表示,而原子用小写字母表示,并用括号来体现层次。几个例子如下图:
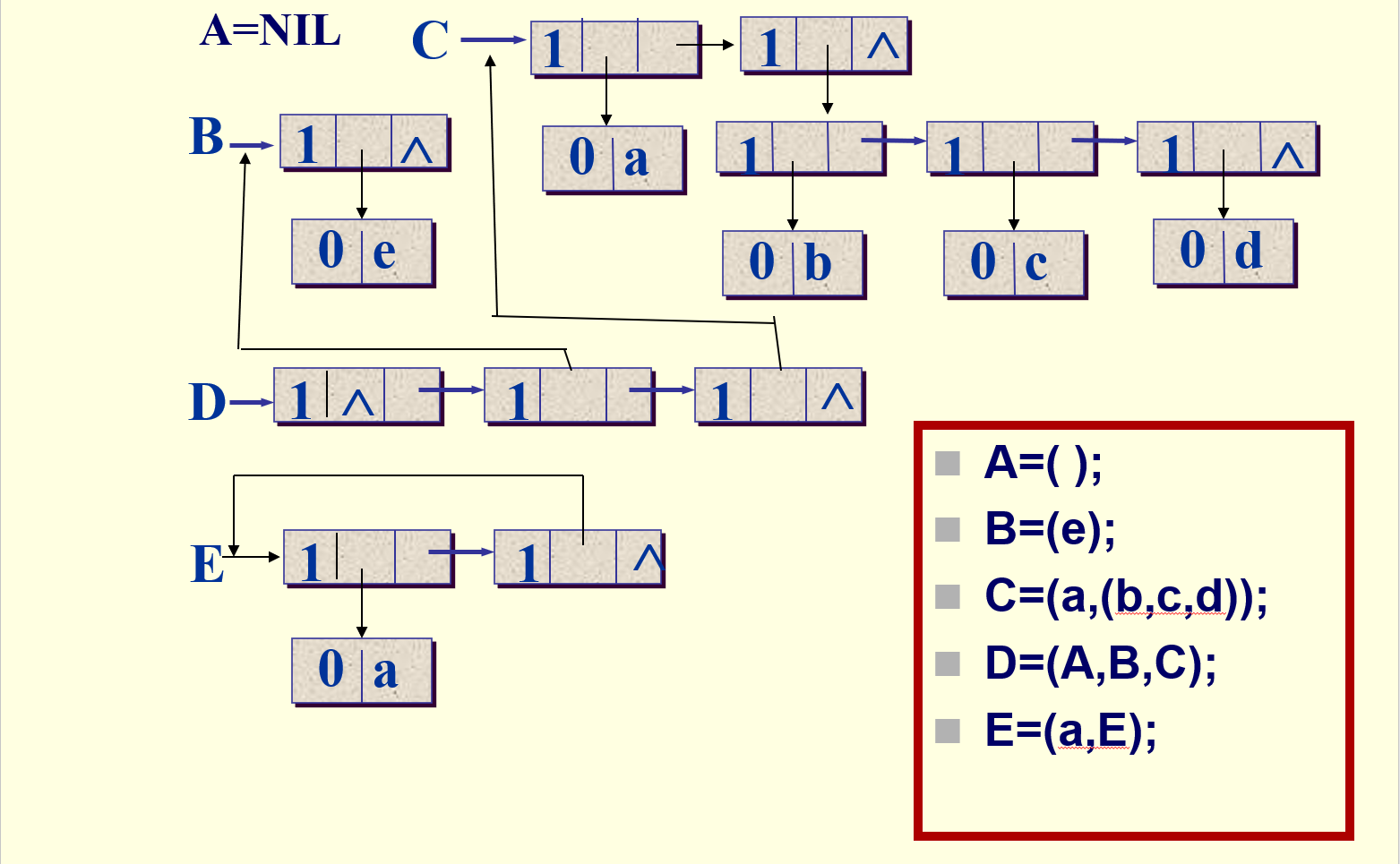
注意,广义表的递归可以没有出口,比如图中E表。
广义表的深度
将广义表的深度定义为所有元素深度的最大值,直观体现就是括号嵌套的最大层数,对于上面的例子,深度如下:A 1, B 1, C 2, D 3, E inf,而这周的编程题便是求广义表的深度。题目如下:
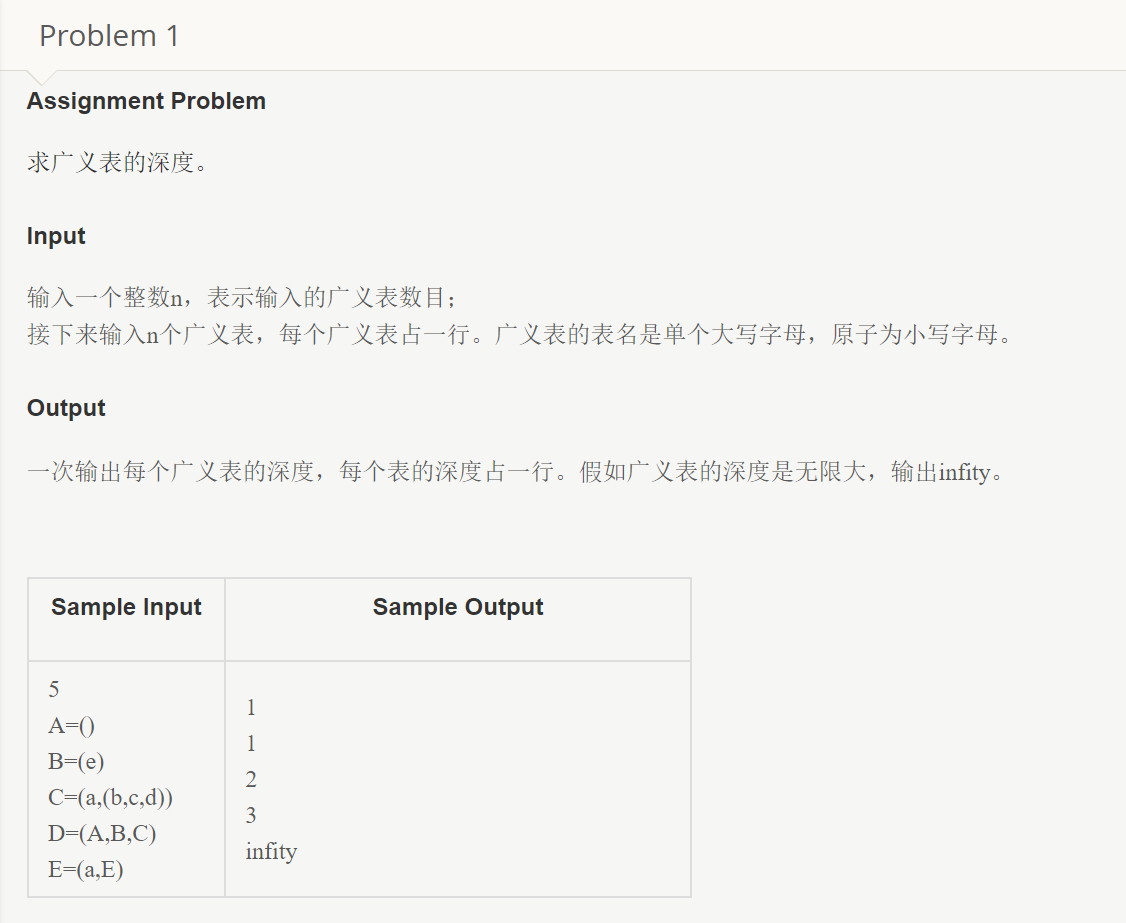
首先考虑每个表中包含的表都在之前输入,那么,我们只需要遍历输入,同时维护一个depth,遇到左括号+1,遇到右括号-1,遇到其他表先加后减,同时在每一步取MAX,最终结果就是这张表的深度,存下来为后面做准备。
然而,未必恰好是这样输入的。很有可能内部的表要在后面输入,比如下面的情况。
应该输出
然而,当我们得到A=(B,C)时,并不知道B和C是什么,也就是说,简单地立即计算行不通了。又该怎么办呢?
方法一——不断遍历
既然不能立即遍历,我们可以这样做:将所有的输入存下来,作为memo,同时构建一张表-深度映射表,每次遍历memo,并尝试计算,如果在计算过程中,发现里面有还没有计算出来的表,说明现在还不能计算,再尝试下一个。如果计算出来,就在memo中删除它,同时将结果存入到表-深度表中。
循环何时结束?每次遍历memo时,我们至少要计算出一个,才有可能继续算下去,否则说明尚未计算的全部算不了了,或者已经计算完毕,这时就可以终止了。尚未计算的,全部都是inf。
具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| #include <bits/stdc++.h>
using namespace std;
int main()
{
vector<char> input;
vector<int> ans(26);
vector<string> memo(26);
int n;
string s;
cin >> n;
for (int i = 1; i <= n; ++i)
{
cin >> s;
input.push_back(s[0]);
memo[s[0] - 'A'] = s.substr(2);
}
bool flag = true;
while (flag)
{
flag = false;
for (char c = 'A'; c <= 'Z'; ++c)
{
bool canSolve = true;
if (memo[c - 'A'] == "")
continue;
for (char d : memo[c - 'A'])
if (d >= 'A' && d <= 'Z' && ans[d - 'A'] == 0)
{
canSolve = false;
break;
}
if (!canSolve)
continue;
int res = 0, depth = 0;
for (char d : memo[c - 'A'])
{
depth += d == '(';
depth -= d == ')';
depth += d >= 'A' && d <= 'Z' ? ans[d - 'A'] : 0;
res = max(res, depth);
depth -= d >= 'A' && d <= 'Z' ? ans[d - 'A'] : 0;
}
ans[c - 'A'] = res;
memo[c - 'A'] = "";
flag = true;
}
}
for (char c : input)
if (ans[c - 'A'])
cout << ans[c - 'A'] << endl;
else
cout << "infity" << endl;
return 0;
}
|
算法分析:这样的计算方法,最坏的情况是每次只计算出最后一个,时间复杂度是O(N^2)的,不过由于大写字母就那么多,实际上运行时间很短,完全可以接受(如果超时,肯定是死循环了)。而写这个代码时,让我想到了大一上学期的消消乐的消去判断逻辑(如何处理连续消去):
- 每次遍历表格,找到所有可以进行消去的地方,然后消去
- 让上面的棋子下落,补充空格,最顶上随机刷新。
重复这个过程,直到某次遍历时,发现没有可以消去的地方,就说明不会再可以消去了。这两个问题的判断逻辑是十分相似的。
方法二——递归求解
同样,我们仍然将输入存入memo,然而,这次我们不是重复尝试,而是遇到谁算谁。比如说,我们看到A=(B,a),就直接去尝试计算B,这样的思路可以用递归体现。而计算方法与上面是相同的。
需要注意的是计算失败的判断:在递归过程中,重复出现了某张表,并且这张表没被算出来过,那么就不可能被算出来了。这样我们返回-1,代表inf。
具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| #include <bits/stdc++.h>
using namespace std;
vector<char> input;
vector<int> ans(26);
vector<int> vis(26);
vector<string> memo(26);
int solve(char c)
{
if (ans[c - 'A'])
return ans[c - 'A'];
if (vis[c - 'A'])
return -1;
vis[c - 'A'] = true;
int res = 0, depth = 0;
for (char d : memo[c - 'A'])
{
depth += d == '(';
depth -= d == ')';
if (d >= 'A' && d <= 'Z')
{
int child = solve(d);
if (child != -1)
res = max(res, depth + child);
else
return -1;
vis[d - 'A'] = false;
}
res = max(res, depth);
}
ans[c - 'A'] = res;
memo[c - 'A'] = "";
vis[c - 'A'] = false;
return ans[c - 'A'];
}
int main()
{
int n;
string s;
cin >> n;
for (int i = 1; i <= n; ++i)
{
cin >> s;
input.push_back(s[0]);
memo[s[0] - 'A'] = s.substr(2);
}
for (char c : input)
{
int res = solve(c);
if (res == -1)
cout << "infity" << endl;
else
cout << res << endl;
}
return 0;
}
|
算法分析:这样的方法,时间复杂度应当是O(N)的(因为每张表最多计算一次),时间复杂度较上面有所改善,不过多了vis数组和递归栈的空间开销。
方法三——拓扑排序
如同最开始所说,如果输入顺序保证了子表在母表之前输入,就省去了繁琐的判断过程了,可以很方便地求解。那么有没有一种方法,可以帮助我们人为地排出计算顺序,来满足上述条件呢?其实,这就是拓扑排序的过程。
拓扑排序最经典的例子就是课程表问题。如果不懂,可以去学习一下,基本上都是这个模板。简单来说,拓扑排序可以解决前置条件问题,即每个问题有若干前置条件,如何安排解决这些问题的顺序,使每个问题都能解决?这道题也符合这个性质:我们可以将母表中包含的子表视为前置条件(因为必须先算出子表),依次进行拓扑排序,最后得到一个计算顺序。注意,不在最终顺序里的,也就是排序失败的,说明出现了互为前提,最后都是inf。
具体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| #include <bits/stdc++.h>
using namespace std;
int main()
{
vector<char> input;
vector<int> ans(26);
vector<string> memo(26);
vector<vector<char>> graph(26);
int n;
string s;
cin >> n;
unordered_map<char, int> indegree;
vector<char> sorted;
for (int i = 1; i <= n; ++i)
{
cin >> s;
input.push_back(s[0]);
indegree[s[0]];
memo[s[0] - 'A'] = s.substr(2);
for (char c : memo[s[0] - 'A'])
if (c >= 'A' && c <= 'Z')
{
++indegree[s[0]];
graph[c - 'A'].push_back(s[0]);
}
}
queue<char> q;
for (auto &p : indegree)
if (p.second == 0)
q.push(p.first);
while (!q.empty())
{
char now = q.front();
q.pop();
sorted.push_back(now);
for (char c : graph[now - 'A'])
{
--indegree[c];
if (indegree[c] == 0)
q.push(c);
}
}
for (char c : sorted)
{
int res = 0, depth = 0;
for (char d : memo[c - 'A'])
{
depth += d == '(';
depth -= d == ')';
depth += d >= 'A' && d <= 'Z' ? ans[d - 'A'] : 0;
res = max(res, depth);
depth -= d >= 'A' && d <= 'Z' ? ans[d - 'A'] : 0;
}
ans[c - 'A'] = res;
}
for (char c : input)
if (ans[c - 'A'])
cout << ans[c - 'A'] << endl;
else
cout << "infity" << endl;
return 0;
}
|
算法分析:拓扑排序时间复杂度是O(n+e),其中n为节点数,e为边数,后续计算时间复杂度为O(N),空间上多了一个辅助栈的消耗。