迷宫问题

本周学习了第三章——栈与队列，作业是一道算法题——迷宫问题，描述如图。

迷宫问题

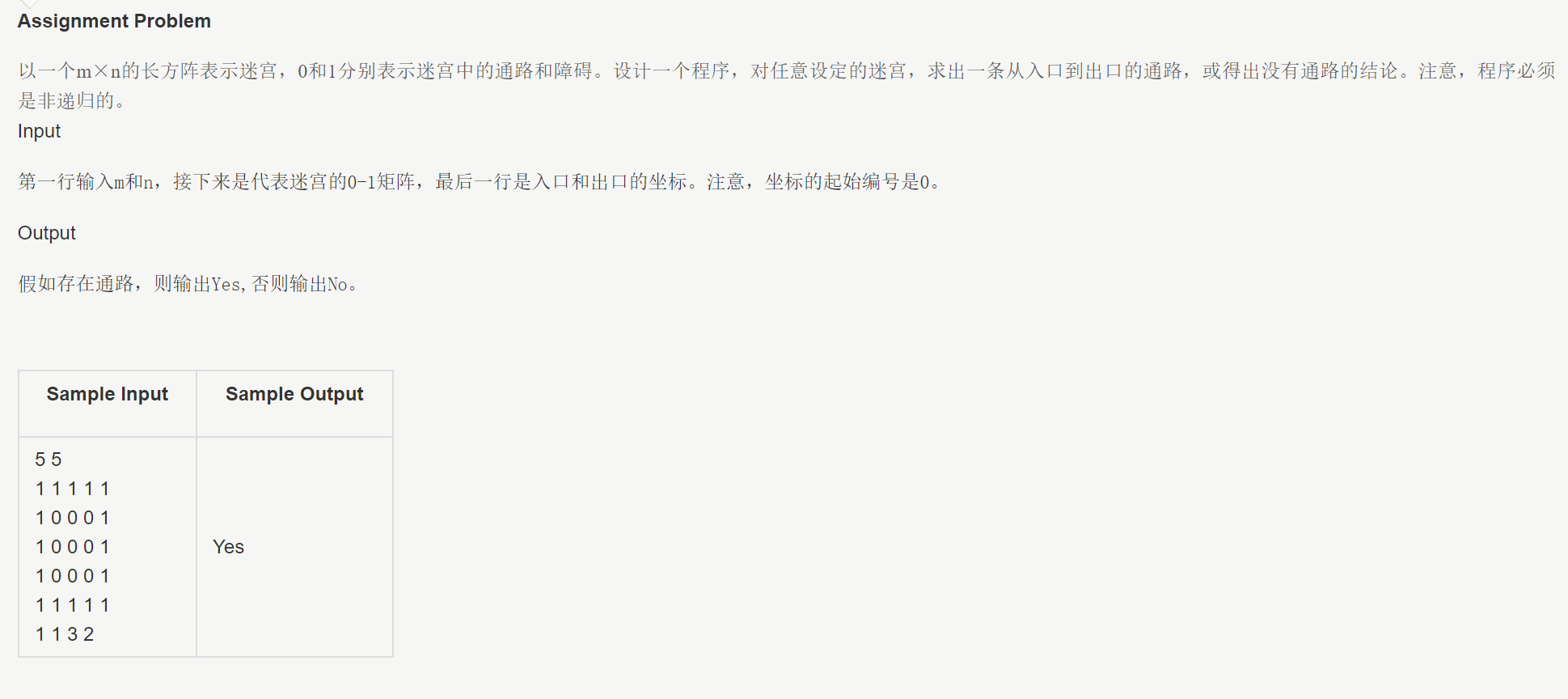
也就是说，要判断是否存在从起点到终点的通路。大体上有广度优先搜索和深度优先搜索两种选择。

由于这章学的是栈和队列，为了用到它们，助教希望我们写出非递归函数（难度确实比递归要高一些，所以后来说写成递归也行）。

递归的深度优先搜索

众所周知，做算法题，越不让用什么，就偏偏用什么，写出来一定是最简单的🤣🤣🤣。所以我们可以首先从递归程序入手，尝试解决这个问题。

首先，显然，我们要读入数据并生成迷宫，记录坐标，不消多说。主要来看一下递归函数怎么写。其实就是dfs模板：当我们搜索到一个点时，如果它就是target，那么就找到了路，直接返回，并且终止搜索；否则，如果它的上下左右有路，就搜索它们（这里要加上判断条件防止越界），也就是递归。同时，每搜索一个点，就将它置为1，防止重复搜索(每个点只需搜索一遍)。

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <vector>
using namespace std;
bool ans = false;
int target_row, target_col;
vector<vector<bool>> grid;
void search(int row, int col) //递归函数
{
    if (row == target_row && col == target_col)
        ans = true;
    if (ans)//找到过路了，直接返回
        return;
    grid[row][col] = 1;//置为1，防止重复搜索
    if (row < grid.size() - 1 && !grid[row + 1][col]) //down
        search(row + 1, col);
    if (row > 0 && !grid[row - 1][col]) //up
        search(row - 1, col);
    if (col < grid[0].size() - 1 && !grid[row][col + 1]) //right
        search(row, col + 1);
    if (col > 0 && !grid[row][col - 1]) //left
        search(row, col - 1);
}
int main()
{
    int m, n, tmp, row, col;
    cin >> m >> n;
    grid = vector<vector<bool>>(m, vector<bool>(n));
    for (int i = 0; i < m; ++i)//生成迷宫
        for (int j = 0; j < n; ++j)
        {
            cin >> tmp;
            grid[i][j] = tmp;
        }
    cin >> row >> col >> target_row >> target_col;
    search(row, col);//从起点开始搜索
    cout << (ans ? "Yes" : "No") << endl;
    return 0;
}

非递归的深度优先搜索

现在考虑如何将递归的dfs转化为非递归的。我们知道，递归时，实际上是程序隐式地使用了一个递归栈来组织运行过程。所以，理论上，所有的递归函数都可以通过等效地把递归栈表示出来来转化为非递归的。那么，这个递归栈中存的是什么呢？应当说，我们的递归函数传了什么，栈中就存什么。在这里，也就是row和col，考虑如何存放它们。最容易想的就是用一个pair<int,int>(C++)捆绑row和col，或者自定义一个struct；另外，还可以通过编解码的方式来组织，一种思路是存放字符串，编码成row#col的字符串形式存入栈中，使用时寻找分隔符的位置得到row和col；另一种思路是在知道0<=row,col<1000时，编码成row * 1000 + col，解码时，num/1000得到row，num%1000得到col。这里只给出存放pair的代码，另外两种只需稍作修改。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
//尝试用pair记录上一次经过的位置
#include <iostream>
#include <stack>
#include <utility>
#include <vector>
using namespace std;
int main()
{
    int m, n, target_row, target_col, tmp, row, col;
    cin >> m >> n;
    vector<vector<bool>> grid = vector<vector<bool>>(m, vector<bool>(n));
    for (int i = 0; i < m; ++i) //生成迷宫
        for (int j = 0; j < n; ++j)
        {
            cin >> tmp;
            grid[i][j] = tmp;
        }
    cin >> row >> col >> target_row >> target_col;
    stack<pair<int, int>> stk;
    stk.push({row, col});
    while (!stk.empty())
    {
        row = stk.top().first;
        col = stk.top().second;
        stk.pop();
        if (row == target_row && col == target_col)
        {
            cout << "Yes" << endl;
            return 0;
        }
        grid[row][col] = 1;                               //标记为1，防止回头
        if (row < grid.size() - 1 && !grid[row + 1][col]) //down
            stk.push({row + 1, col});
        if (row > 0 && !grid[row - 1][col]) //up
            stk.push({row - 1, col});
        if (col < grid[0].size() - 1 && !grid[row][col + 1]) //right
            stk.push({row, col + 1});
        if (col > 0 && !grid[row][col - 1]) //left
            stk.push({row, col - 1});
    }
    cout << "No" << endl;
    return 0;
}

有一个问题需要说明一下，这里是dfs还是bfs呢？初看可能会觉得，这个过程是每次将四周入栈，似乎是每次向外搜索一圈的广度优先搜索。然而，dfs和bfs是以访问顺序来区分的。尽管我们将四周全部入栈了，但是我们只访问栈顶，栈顶的四周又会入栈……如此循环往复，我们永远只访问四周中的一个，直到找到目标或者不再有解空间。这种先沿一条路走到黑，不行再回头的过程，无疑是深度优先搜索。

广度优先搜索

考虑这样的附加问题：如果我们不仅仅是要判断有无通路，在有通路时，还要给出到达终点的最小步数，该怎么做呢？这可以通过bfs实现，从起点出发，每次向外探索一圈，产生一系列新的点；在下一轮中，这些点都将被访问。这样蔓延开来，第一次触及终点经历的轮数就是最短步数。由于我们要区分此轮和上轮的点，需要一个先入先出的结构，在某轮初始时获取大小cnt，弹出并访问cnt个队首，就是上一轮的所有点了。代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//用队列进行广度优先搜索，同时，如果有出口，还可以给出最小步数
#include <bits/stdc++.h>
using namespace std;
vector<vector<bool>> grid; //迷宫
queue<pair<int, int>> q;   //bfs的辅助队列
void enQueue(int r, int c)
{
    grid[r][c] = 1; //入队时即置为1，防止重复入队引发tle
    q.push({r, c});
}
int main()
{
    int m, n, target_row, target_col, tmp, row, col;
    cin >> m >> n;
    grid = vector<vector<bool>>(m, vector<bool>(n));
    for (int i = 0; i < m; ++i) //生成迷宫
        for (int j = 0; j < n; ++j)
        {
            cin >> tmp;
            grid[i][j] = tmp;
        }
    cin >> row >> col >> target_row >> target_col;
    enQueue(row, col);
    while (!q.empty()) //每次向外探索一圈，置为1并入队
    {
        int cnt = q.size();
        for (int i = 1; i <= cnt; ++i)
        {
            row = q.front().first;
            col = q.front().second;
            q.pop();
            if (row == target_row && col == target_col)
            {
                cout << "Yes" << endl;
                return 0;
            }
            if (row < grid.size() - 1 && !grid[row + 1][col]) //down
                enQueue(row + 1, col);
            if (row > 0 && !grid[row - 1][col]) //up
                enQueue(row - 1, col);
            if (col < grid[0].size() - 1 && !grid[row][col + 1]) //right
                enQueue(row, col + 1);
            if (col > 0 && !grid[row][col - 1]) //left
                enQueue(row, col - 1);
        }
    }
    cout << "No" << endl;
    return 0;
}

leetcode 1926. 迷宫中离入口最近的出口就采用了这样的方法。根据该题修改过的代码也成功通过了